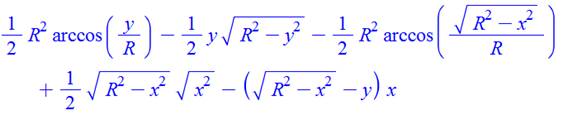|
||||||||||||||||||||||||||||||||||||||||
![]()
|
RECTANGLE
et CERCLE Cas d'intersection dans un quadrant
Nous rappelons que nous
considérons l'intersection d'un disque avec un rectangle de grande dimension qui
glisse vers la droite. Dis autrement, le coin bas-droit du rectangle est dans
le quadrant haut-gauche du disque. Ou, toutes les autres configurations du
même type obtenues par rotation ou symétries.
|
|
|
|||
|
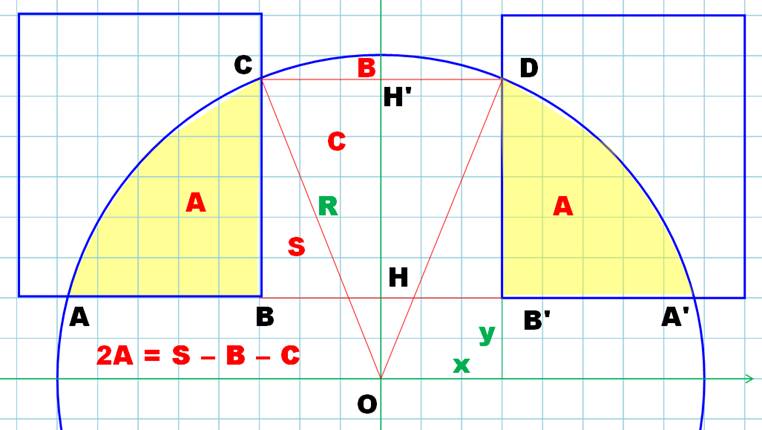
Calcul de l'aire de A (en jaune sur la figure), intersection ABC d'un
rectangle avec le cercle dans un seul
quadrant. Nous dessinons son
symétrique A'B'D de sorte que: 2A = Aire S du segment AA'DC – Aire
centrale BB'DC et
Aire centrale = aire C du rectangle BB'DC + aire B du segment CDH' En bref: 2A = S – (B + C)
|
|||
|
Pour info: aire du demi-cercle de rayon 8 |
|
= 100,53… |
|
|
|
S = 68,86… |
||
|
Dans le triangle OCH' |
h² = OH'² = R² – x² |
h = 7,41… |
|
|
Aire du segment B |
|
B = 2,35… |
|
|
Largueur du rectangle BB'DC |
L = HH' = OH' – OH |
L = 5,41… |
|
|
Aire du rectangle |
|
C = 32,49… |
|
|
Aire de l'intersection A |
A = ½ (S – B – C) |
A = 17,01… |
|
|
Formule
complète
|
|||
Voir Abaque
|
Connaissant
l'aire du segment ce calcul est relativement simple. La seule petite
difficulté est le calcul de l'arc cosinus x qui est l'angle en radians tel
que son cosinus est égal à x. Une calculette fera l'affaire
avec la fonction inverse du cosinus. Certes,
les calculs sont copieux, surtout si on a besoin de nombreuses évaluations.
Un abaque peut parfois suffire. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/RectangT.htm |
![]()