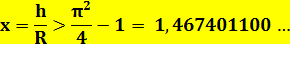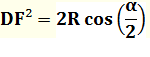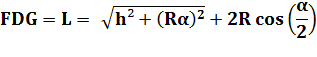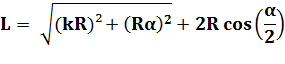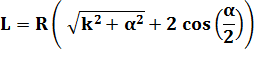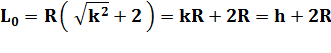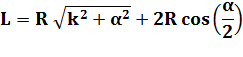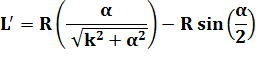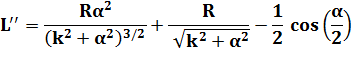|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CYLINDRE PLEIN – Trajet de la Fourmi
Comment déterminer les
distances sur un cylindre? Quelle est la longueur la
plus courte d'un point à un autre? Énigme de la fourmi qui se
dirige au plus vite vers une goutte d'eau en circulant sur un récipient plein
(avec couvercles). |
|
1.
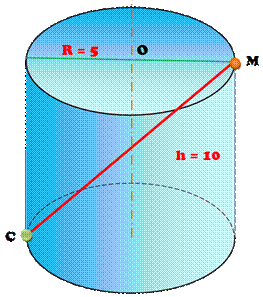
Une mouche
est sur le bord supérieur d'un cylindre creux
de 5 cm de rayon et 10 cm de hauteur. Elle avise une perle de confiture sur
le bord inférieur à l'opposé. Quelle est
la distance minimale qu'elle devra faire pour pomper la confiture ? 2.
Si une fourmi était à sa place que
ferait-elle pour minimiser son trajet? 3.
Si le cylindre est fermé à ses extrémités
(couvercles), que ferait la fourmi? |
|
|
||
|
Énigme Une
fourmi se trouve sur l'extérieur d'un cylindre plein
(comme une boite de conserve fermée). Elle est
en haut au point F et veut se rendre au point G en bas, mais diamétralement
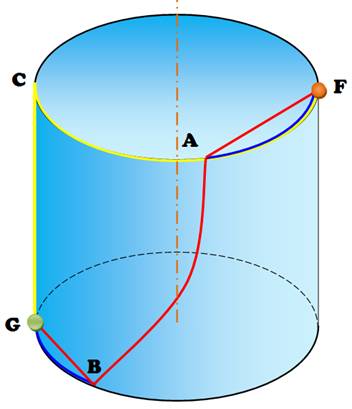
opposé Approche Une première
observation montre que parmi les trajets possibles, la fourmi a intérêt à
prendre le chemin rouge pour minimiser le trajet.
Plusieurs questions se posent:
|
Illustration
|
|
Voir tout de suite la Solution
|
|
||
|
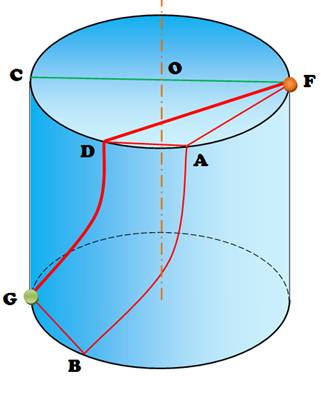
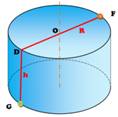
Plutôt
que de faire le trajet sur le bas du cylindre BG),
la fourmi peut faire l'équivalent sur le haut (AD), sans changer la longueur
parcourue. Il
devient évident, qu'alors, il est possible d'optimiser le trajet FAD en prenant la ligne droite FD. Le trajet
à considérer est donc FDG
En développant le cylindre, le trajet courbe DG
est minimum si c'est une ligne droite une fois le cylindre développé (un
morceau de spire d'une hélice circulaire). |
|
|
|
|
||
|
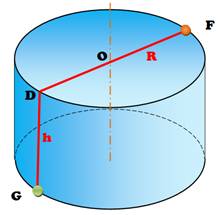
Si la
hauteur du cylindre est petite devant le rayon (figure de gauche), le trajet est tout simplement un diamètre,
suivi d'une descente verticale. L = 2R + h Mais dans
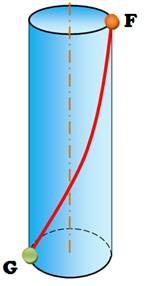
quelles conditions pour h/R ? La réponse n'est pas simple. Si la
hauteur du cylindre est très grande devant le rayon (figure de droite), le trajet tend vers la descente sur une
spire. |
|
|
|
|
||
|
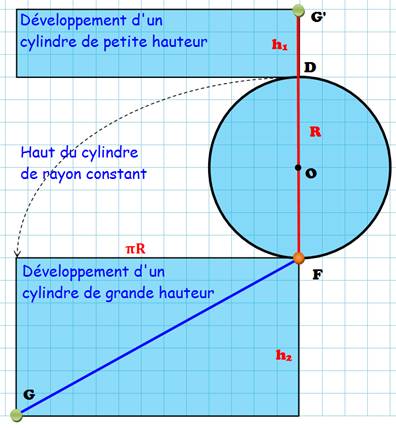
Prolongeons
notre raisonnement avec le développement du cylindre. Si la
hauteur est très petite (rectangle en
haut), la fourmi à plus vite fait de parcourir le diamètre du couvercle
et descendre tout droit vers son but: FODG'. Son
trajet mesure: L1 = 2R + h Si la
hauteur est très grande (rectangle en
bas), la fourmi a intérêt à descendre tout de suite sur une spire, en
fait une droite sur le développement: FG. Son trajet mesure: La
question: quand la fourmi doit-elle opter pour l'un ou l'autre des trajets? Dans la
mesure où il s'agit de longueur (valeurs positives), nous pouvons comparer
les carrés. |
|
|
|
L1² L2² |
|
|
|
Prenons L1>L2
⇨ |
|
|
|
Trajet en latéral (h > 1,467 R)
|
Trajet en horizontal et
vertical (h < 1,467 R)
|
|
|
||
|
Comment
confirmer que les deux cas exprimés ci-dessus sont en fait la solution de ce
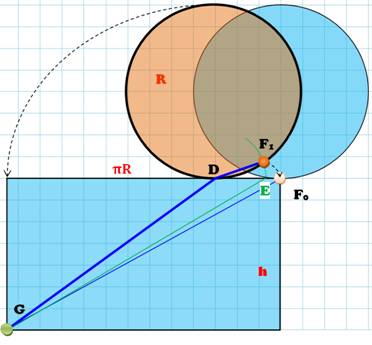
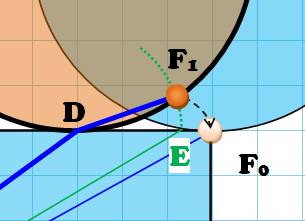
problème? Trajet en latéral Faisons
tourner un peu le cercle. Au lieu du
trajet direct F0G, la fourmi part de F1 arrive au bord
en D et repart en oblique vers G. Le point
F1 est développé au point F0. Autrement-dit: DF0 = arc DF1. Le point
E est tel que DE = corde DF1. La
longueur de la corde est inférieure à celle de l'arc; le point E est situé
entre D et F0. Le
nouveau trajet de la fourmi (GDF1) est de même longueur que le
trajet à GDE. Il est plus long que l'oblique GE. Mais GE
est plus long que GF0. Conclusion Pas
possible de conclure! Il est
nécessaire de passer à une solution analytique. Calcul de minimum d'une
fonction en passant par la dérivée. |
Zoom
|
|
|
|
||
|
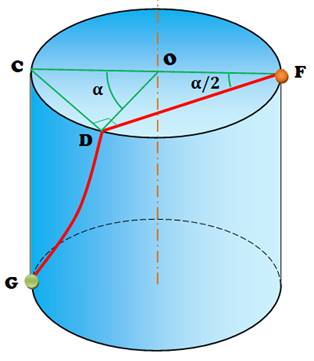
Remarquez que l'angle DOC (alpha) est le double de l'angle pris par la
fourmi (DFC). L'angle
alpha permet d'apprécier la longueur de l'arc CD = R Et, la longueur de la spire est égale à
Dans le
triangle rectangle FCD
|
|
|
|
Longueur
du trajet complet avec h =
k R |
|
|
|
Vérification
pour alpha = 0 |
|
|
|
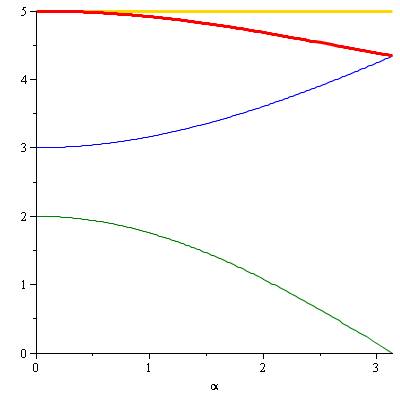
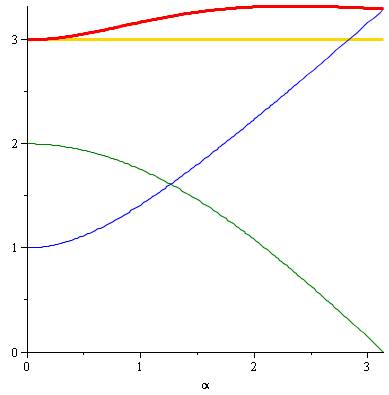
Allure de
cette fonction avec R =
1 et k = 3 (h = 3). Comparaison
à L0. L est en
rouge. Départ en 5 et arrivée en
Pour
alpha (angle au centre) de 0 à Pi, la valeur de la distance L (rouge) est
inférieure à la longueur du trajet (jaune). Elle est minimale pour alpha =
Pi. La fourmi a intérêt à prendre directement le chemin oblique En bleu,
contribution du terme en racine; En bleu,
contribution du terme en cosinus. |
|
|
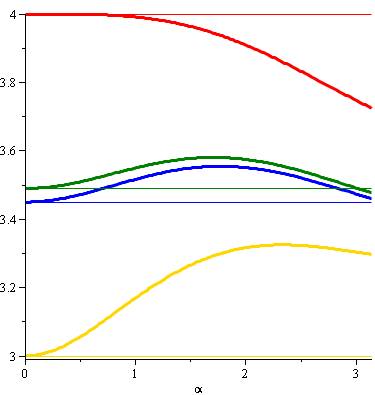
Allure de
la fonction pour R =
1 et k = 1 (h =1). Nous
avons que k = 1,467… est une valeur critique. Effectivement,
en passant de k = 3 à k = 1, la courbe rouge est désormais en haut de la
droite jaune. Quelle que
soit la valeur de l'angle alpha de 0 à Pi, la distance en rouge est plus
grande que la distance en jaune. La fourmi a intérêt à prendre le chemin
direct. Nous
confirmons avec ces deux exemples qu'il existe bien deux situations
possibles. |
|
|
Étude de
la zone de transition Valeur de
k: k =
2 rouge k =
1,49 verte k = 1,467… non représentée k =
1,45 bleue k =
2 jaune La courbe représente la longueur du trajet en oblique selon l'angle alpha,
alors que la droite représente la longueur
du trajet direct. Observez
que la courbe bleue ne coupe pas la droite bleue, alors que la courbe verte
coupe la droite verte. Or, pour ces deux courbes k et de part et d'autre de
la valeur de transition. Nous
confirmons la valeur de transition calculée à 1, 467 … |
|
|
La
démonstration formelle passe par l'analyse des dérivées première est seconde. Recherche
de maximums locaux qui montrent que les valeurs minimums de distance sont
atteintes pour les deux valeurs extrêmes de l'angle alpha. Solution
complète dans le livre indiqué en référence |
|
|
Avec
un cylindre creux la solution géométrique comme la
solution analytique (plus compliquée) donnent la solution. Pour
le cylindre plein, le problème est de difficulté
supérieure. Seule la solution analytique (à ma connaissance) donne la
solution. Une approche géométrique suivie d'une analyse
expérimentale permet néanmoins d'atteindre la solution. |
![]()
|
Réponse: La
mouche vole en ligne droite du point M au
point C. MC²
= 10² + 10² = 200 MC
= 14,14… cm 2)
S'il s'agit d'une fourmi avec le cylindre creux, elle suivra une trajectoire oblique à
l'intérieur du cylindre le long d'une spire d'hélice dont la longueur est: arcMC²
= 10² + ( 3)
Avec un cylindre fermé, la fourmi, dans ce cas particulier, la fourmi
suivra également la spire comme en 2). Mais il existe des cas où elle aurait
plutôt intérêt à filer le long d'un diamètre et descendre tout schuss. >>> |
Retour
/ Cas du trajet sur une boite parallélépipédique
![]()
|
Retour |
|
|
Suite |
|
|
Aussi |
|
|
DicoNombre |
|
|
Livre |
|
|
Cette page |
![]()