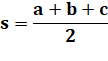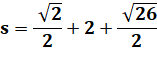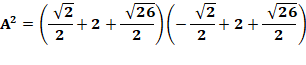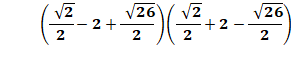|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
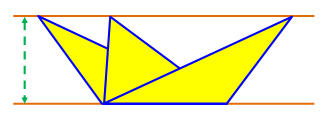
Problème de l'aire d'un triangle dans quatre carrés Application simple, mais
astucieuse du calcul de l'aire d'un triangle. Tous les triangles ayant même
base et un sommet situé sur une parallèle à la base ont
même aire. Oui, car, ils ont la même hauteur.
|
|
|
||
|
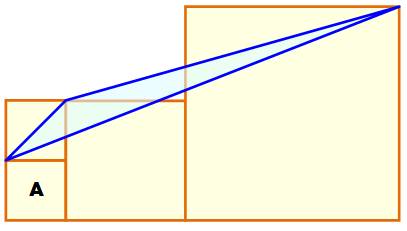
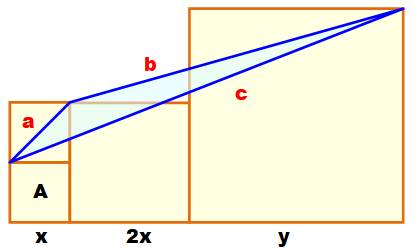
Quatre
carrés disposés comme indiqué. Les plus
petits ont une aire égale à A. Quelle
est l'aire du triangle bleu ? |
|
|
|
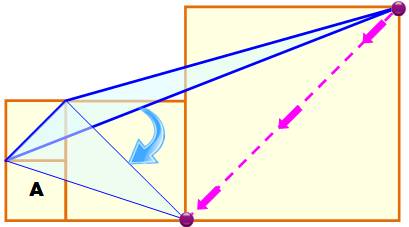
Trouvons un
triangle d'aire équivalente. La
diagonale du grand carré est parallèle à celle du petit carré qui se trouve
être un côté du triangle. Le sommet
éloigné de ce côté est translaté le long de la diagonale jusqu'en bas, tout
en conservant, donc, son aire. Les deux
triangles bleus ont même aire. |
|
|
|
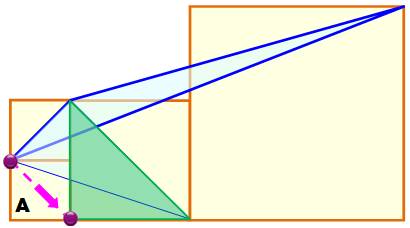
Renouvelons
l'opération avec la diagonale du petit carré inférieur. Le sommet
gauche est translaté sur la diagonale jusqu'en bas; le triangle conserve son
aire. Le
triangle vert a même aire que le triangle de départ. L'aire du
carré central est égale à 4A. L'aire du
triangle est égale à 2A. Remarquez que la taille du carré de droite peut être
quelconque. |
|
|
Voir Brève
923
|
|
||
|
Utilisation
de la formule
de Héron pour calculer l'aire :
|
|
|
|
Longueur
des côtés |
|
|
|
Calcul
avec x = 1 et y = 2 Ceci est
une vérification et non pas une démonstration |
|
|
|
Demi-périmètre |
|
|
|
Aire
(tous calculs faits) En
reprenant les calculs avec d'autres valeurs de x et de y, on retrouve bien
notre formule. |
A = 2 = 2x2 |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Exercice/CarrQuat.htm |
![]()