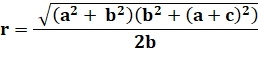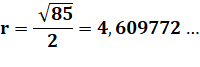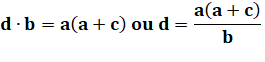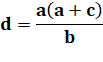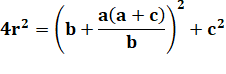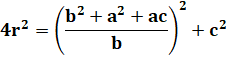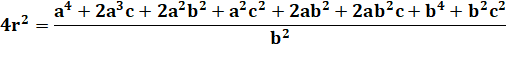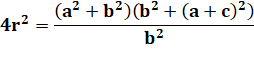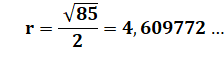|
Édition du: 08/05/2023 |
|
INDEX |
Énigmes en géométrie |
||
|
Exercices 01 |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
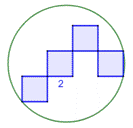
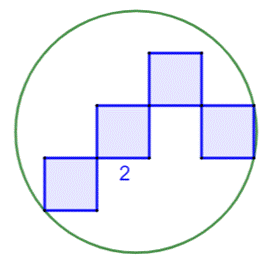
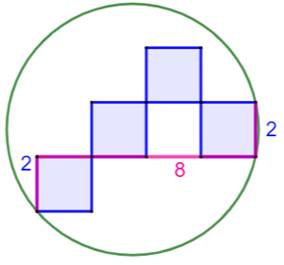
Résoudre cette
énigme dont la solution est bien cachée par un escalier formé de quatre
carrés. Quel est le rayon du cercle vert ? |
||
|
|
Sommaire de cette page >>> Escalier dans le cercle >>> Application à l'énigme |
Débutants Glossaire |
|
Problème Montrer que le rayon du cercle vert vaut:
Avec les valeurs numériques
|
|
|||||||||||
|
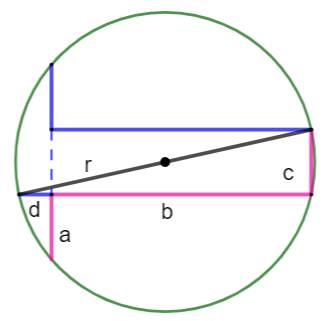
Construction Construire le symétrique de l'escalier d'origine
(bleu). Introduction du segment d prolongeant la marche
b. Le théorème des cordes
sécantes nous fournit cette équation:
Les segments b et c sont à angle droit. Le
triangle qui les porte est rectangle et l'hypoténuse est donc un diamètre,
qui mesure 2r.
|
|
|||||||||||
|
Calcul
|
||||||||||||
|
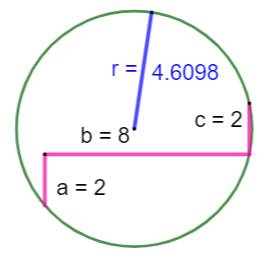
Quel est le rayon du cercle vert ?
|
Application du calcul de l'escalier
selon le tracé rose.
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Exercice/EscaCer.htm
|