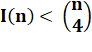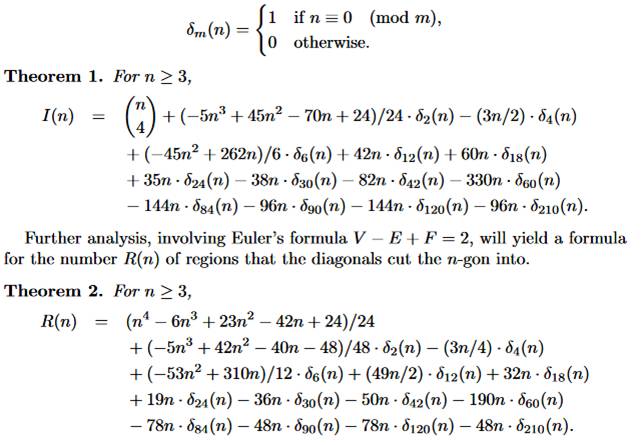|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
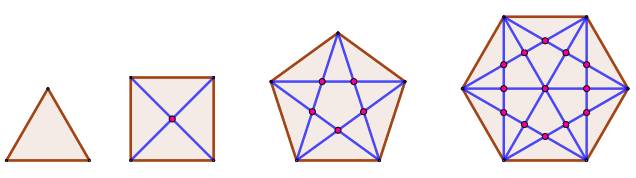
DIAGONALES des POLYGONES Quantité régions et d'intersections On sait compter
les diagonales du polygone régulier. Celles-ci partagent l'intérieur du
polygone en régions. Combien ? Et, combien
d'intersections des diagonales. |
Voir Noms
des polygones / Longueurs
des diagonales
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
Voir Brève
519
|
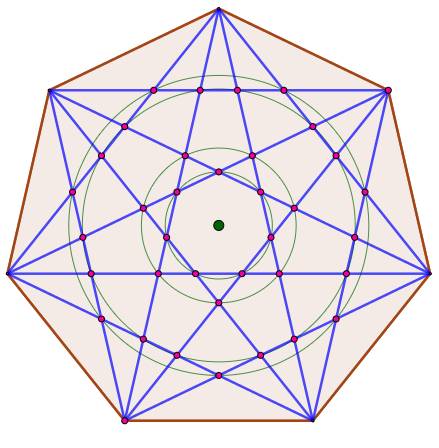
Heptagone Le centre
(vert) des cercles passant par les points d'intersections des diagonales est
distinct. Les 35 intersections
sont toutes simples: croisement de deux diagonales: 35 I2 . La
quantité d'intersections est un multiple de 7 (35 = 7 x 5). |
|
|
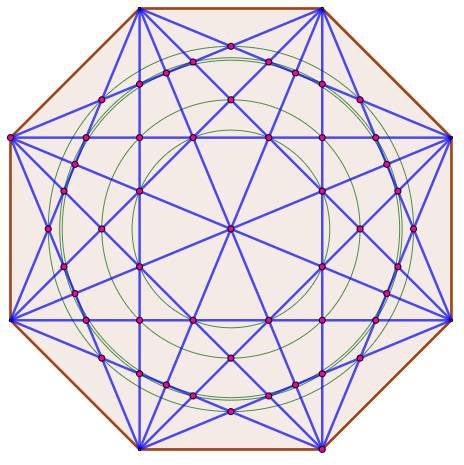
Octogone Le centre
des cercles est l'un des points d'intersections. Les 49
intersections sont simples ou multiples:
La
quantité d'intersections moins 1 est un multiple de 8 (49 – 1 = 48 = 8 x 6). Intersection record Pour un
polygone régulier, il est impossible d'avoir plus de 7 diagonales qui se
rencontrent en un seul point autre que le centre. Et ce cas
se rencontre pour n multiple de 30. |
|
Cas du 30-gone ou triacontagone
|
|
|
|
|
||
|
Maximum |
En effet,
quatre points définissent deux diagonales et une intersection. Sauf que
certains points sont communs. le calcul n'est pas simple ! |
|
|
Formules |
Extrait de l'article de Bjorn
Poonen and Michael Rubinstein |
|
|
intersections |
I(n) = 0, 0, 0, 1, 5, 13, 35, 49, 126, 16110, 330, 301,
715, 757, 1365, 1377, 2380, 1837, 3876, 384120,
5985, 5941, 8855, 7297, 12650, 12481, 17550, 17249, 23751, 1680130, 31465, 30913, 40920, 40257,
52360, 46981, 66045, 64981, 82251, 8088140,
101270, … Si n est pair alors
I(n) – 1 est divisible par n. Si n est impair
alors I(n) est divisible par n. |
|
|
Régions |
R(n) = 0, 0, 1, 4, 11, 24, 50, 80, 154, 22010, 375, 444, 781, 952, 1456, 1696,
2500, 2466, 4029, 450020, 6175,
6820, 9086, 9024, 12926, 13988, 17875, 19180, 24129, 2148030,
31900, 33856, 41416, 43792, 52921, 52956, 66675, 69996, 82954, 8680040, 102050, … |
|
Cas du
41-gone dont les régions sont colorisées – Extrait

Source image: Scott R. Shannon, Colored illustration for n = 41
(3rd version) – cité par A007678
Allez vers ces liens pour obtenir l'image complète et
bien d'autres
|
|
|
|
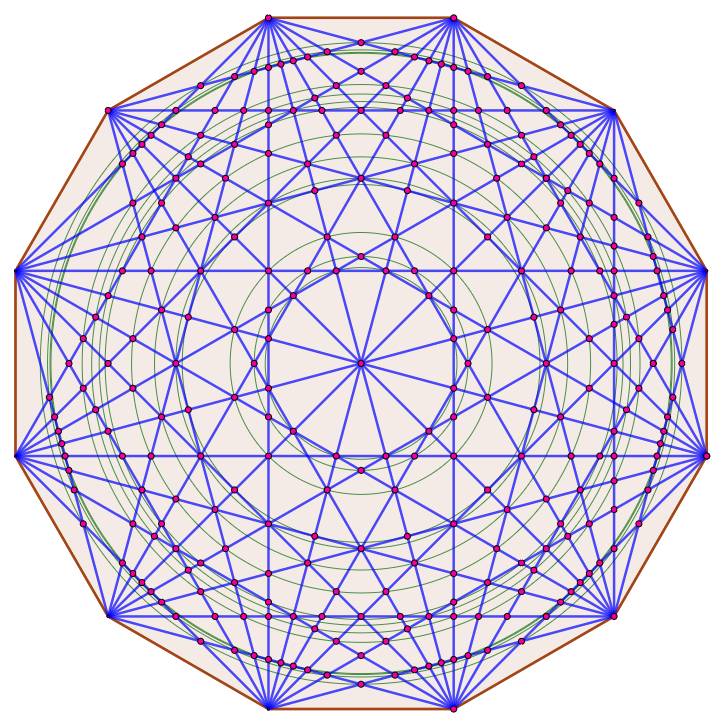
La
quantité d'intersections pour n = 11, 12, 13 semble erratique: 330,
301, 715. Voyons le cas de n
= 12 (dodécagone) qui semble
régresser. Comptons les intersections
en rouge sur les cercles verts.
À partir
d'un faisceau issu d'un sommet, on compte pour le premier amas (2, 2, 2, 1),
pour l'amas de cercles suivant (2, 2, 1, 2) puis (2, 1, 2, 1) et (1, 2, 1). Soit un total de 25
intersections par faisceau-sommet, à multiplier par 12, plus l'intersection
centrale: |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/TrgRegio.htm
|
![]()