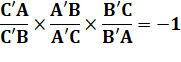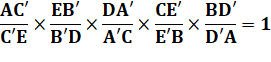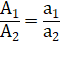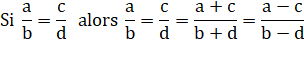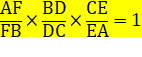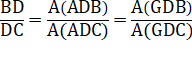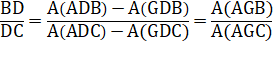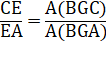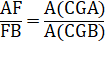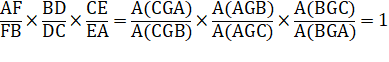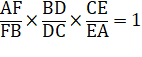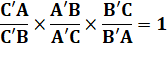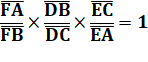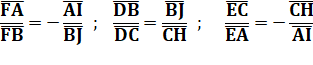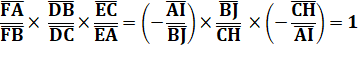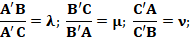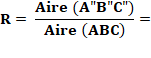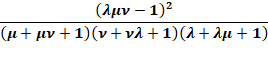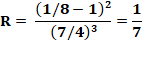NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/02/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Isométriques	Droites et points	Hauteurs	Médianes
	Point Milieu		Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
	Aire = Aire	Quatre triangles	Heilbron	Carrés triangles
	Résolution	Représentation	Brocard	Cercles et triangles
		Sommaire de cette page >>> DROITES particulières dans le triangle >>> CÔTÉS >>> CÉVIENNES: médianes, hauteurs et bissectrices >>> MÉDIATRICES >>> THÉORÈME DE CEVA >>> THÉORÈME DE MÉNÉLAÜS d'Alexandrie >>> BARYCENTRE

Voir Propriétés fondamentales des triangles

Droites et points dans le TRIANGLE

Intimité des triangles: points et droites remarquables.

DROITES PARTICULIÈRES dans le triangle
CÔTÉ SOMMET	Chacun des trois segments limitant un triangle. Chacun des trois points de jonction des côtés.
HYPOTÉNUSE CATHÈTE BASE	Côté opposé à l'angle droit dans un triangle rectangle. Chacun des côtés de l'angle droit d'un triangle rectangle. Côté adjacent aux deux côtés égaux du triangle isocèle. Suite >>>
CÉVIENNE MÉDIANE HAUTEUR BISSECTRICE	Droite qui passe par le sommet d'un triangle. Cévienne joignant le milieu du côté opposé. Cévienne perpendiculaire au côté opposé. Cévienne bissectrice de l'angle (intérieur ou extérieur). Suite >>>
MÉDIATRICE	Médiatrice de chaque côté. Suite >>>
BROCARD	Création d'un angle constant avec les céviennes. Suite >>>

CÔTÉS du triangle
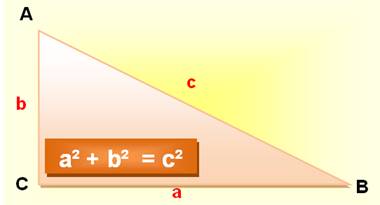
Triangle quelconque CÔTÉS: segment délimitant la surface du triangle Triangle rectangle HYPOTÉNUSE: côté opposé à l'angle droit CATHÈTE: chacun des côtés de l'angle droit (peu utilisé) Triangle isocèle BASE: côté adjacent aux deux côtés égaux	Triangle quelconque Au côté le plus grand est opposé l'angle le plus grand La longueur de chaque côté est comprise entre la valeur absolue de la différence des deux autres et leur somme (formule de Ceva) b – c < a < b + c Triangle rectangle Le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés (cathètes). Théorème de Pythagore Triangle isocèle Les deux angles à la base sont égaux

CÉVIENNES
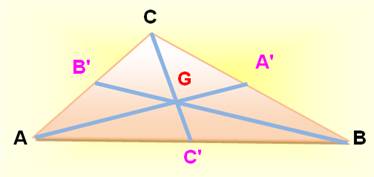
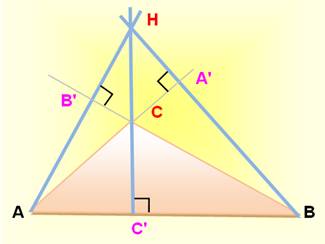
Triangle quelconque CÉVIENNE: droite qui passe par le sommet d'un triangle. Médianes, Hauteurs et Bissectrices sont des céviennes particulières. Les médiatrices ne sont pas des céviennes. MÉDIANE: cévienne joignant le milieu du côté opposé. Les trois médianes sont concourantes en G, centre de gravité du triangle. G est situé au 2/3 à partir du sommet de chaque médiane. HAUTEUR: cévienne perpendiculaire au côté opposé. Les trois hauteurs sont concourantes en H, l'orthocentre du triangle. 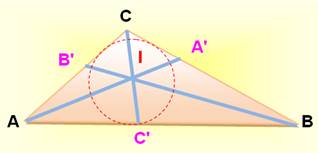BISSECTRICE: cévienne bissectrice de l'angle (intérieur ou extérieur). Les trois bissectrices intérieures sont concourantes en I, le centre du cercle inscrit dans le triangle. Une bissectrice intérieure et les deux bissectrices extérieures concourent en un même point, le centre d'un des trois cercles exinscrits du triangle.	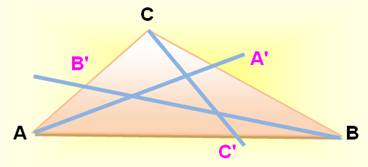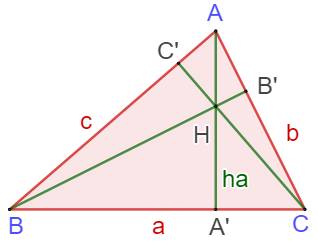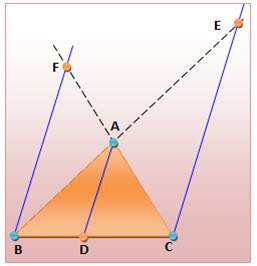Trois céviennes quelconques dans ce triangle: AA', BB' et CC' Suite en Céviennes Médianes Suite en Médianes Hauteurs Suite en Hauteurs Bissectrices intérieures Suite sur les bissectrices extérieures

Voir Théorème des céviennes régulières dans le triangle quelconque/ Théorème des angles des céviennes

MÉDIATRICES
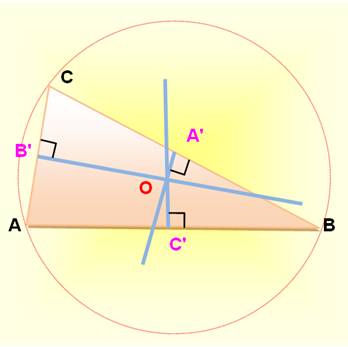
Triangle quelconque MÉDIATRICE: Médiatrice de chaque côté. Les trois médiatrices sont concourantes en O, le centre du cercle circonscrit au triangle.	Médiatrices Suite en Médiatrices Voir Médiatrices, hauteurs et médianes

THÉORÈME DE CEVA (1648-1734)
En 1678, Giovanni Ceva publie son théorème.  Généralisation aux polygones à nombre impair de côtés.	Triangle quelconque Condition nécessaire et suffisante pour que les trois céviennes soient concourantes: Voir Hauteurs concourantes – Démo Pentagone Dans le pentagone 5 droites issues des sommets sont concourantes si et seulement si:
Théorème des perpendiculaires aux côtés Soit trois droites perpendiculaires AA', BB' et CC' (pas nécessairement les hauteurs, a priori). Ces trois droites sont concourantes si et seulement si: BA'² + CB'² + AC'² = A'C² + B'A² + C'B² Dans le cas des hauteurs, et avec le théorème de Pythagore, on a: G = c² – ha² + a² – hb² + b² – hc² D = b² – ha² + c² – hb² + a² – hc² La partie gauche (G) est bien égale à la partie droite (D). Les hauteurs sont concourantes.

Concours des céviennes – Démonstration
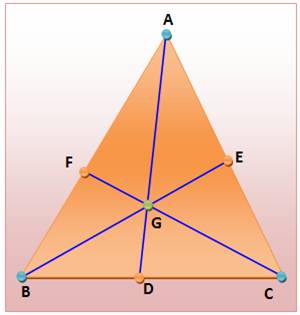
Trois droites issues des sommets du triangle : ce sont des céviennes. Propriétés utilisées 1) Aire des triangles de part et d’autre de la hauteur L’aire A d’un triangle est égal à ½ a.h Avec h un des hauteurs. Celle-ci partage le triangle en deux petits triangles dont les aires sont : A1 = ½ a1.h et A2 = ½ a2.h Ou en faisant le rapport : 2) Propriété des proportions Démonstration		Théorème de Ceva Si les céviennes sont concourantes alors :
Les triangles ADB et ADC ont même hauteur ; de même que DB et GDC :
Nous pouvons retrancher
Idem pour les deux autres
Produit des trois
Réciproque du théorème de Ceva	Trois points (D, E et F), chacun sur un des côtés d’un triangle (ABC), et distinct des sommets, alors les droites AD, BE et CF sont concourantes ou parallèles si :
Céviennes parallèles La propriété reste valable même si les céviennes sont parallèles et le point de concours est « rejeté » à l’infini.

THÉORÈME DE Ménélaüs d'Alexandrie (fin du premier siècle)
Proche du théorème de Ceva Trois points A', B' et C' placés sur les côtés d'un triangle quelconque. La condition nécessaire et suffisante pour que ces trois points soient alignés est exprimée par la formule indiquée sous la figure. Voir Théorème de Pappus / Homologie

Théorème de Mènèlaüs – Démonstration
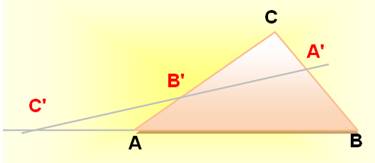
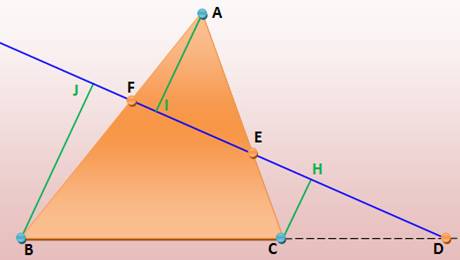
Un triangle ABC et trois points (D, E et F) sur chacun des côtés, distincts des sommets. Théorème de Mènélaüs Ces trois points sont alignés si : Démonstration Elle nécessite : De supposer les trois points alignés ; D’effectuer le tracé des perpendiculaires à la droite DEF ; et
D’appliquer le théorème de Thalès.
En multipliant :
Réciproque	Si les trois points sont alignés, alors la relation est vérifiée.

Théorème de ROUTH (1879)
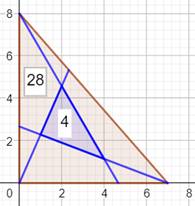
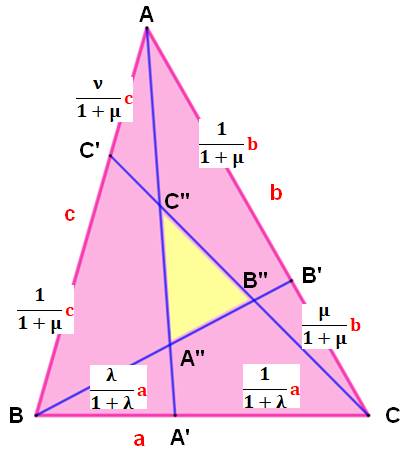
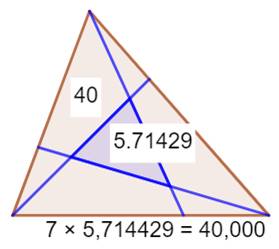
Construction Triangle quelconque ABC. Céviennes AA', BB' et CC. Rapports: Théorème de Routh Exemples A', B', C' milieux des côtés: Aire nulle car . Oui, les médianes sont concourantes. A', B', C' au 1/3 des côtés, alors et l'aire vaut 1/7 (Illustration). Calcul Autre exemple avec 7 x 4 = 28	Cas où les pieds des céviennes sont aux 1/3

Voir Edward John Routh (1831-1907) et contemporains

BARYCENTRE
Tous les points remarquables d'un triangle peuvent être définis comme un barycentre avec les pondérations adéquates. Les coordonnées barycentriques permettent de traiter les propriétés du triangle par calcul matriciel.

Suite	Droite d'Euler Droite de Simson Points, droites, cercles dans le triangle
Voir	Triangle – Index Triangle – Glossaire Éléments de géométrie Triangle – Débutants, novices DicoMot DicoNombre
Site	Théoréme de Ceva – Wikipédia
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/DroiPoin.htm