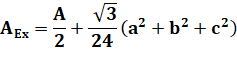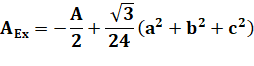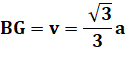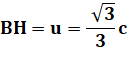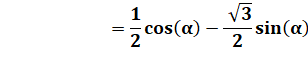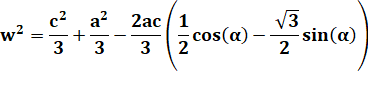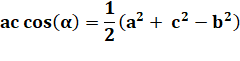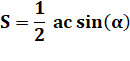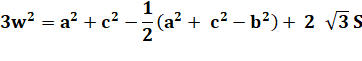|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
THÉORÈME NAPOLÉON Triangles Napoléon / Points
Napoléon Présentation du triangle dit
Napoléon et démonstrations du théorème Napoléon: la construction produit des
triangles internes et externes qui sont équilatéraux.
Les centres de gravité sont confondus avec celui du triangle original. Napoléon était amateur de
géométrie, mais aucune preuve ne permet de dire qu'il est à l'origine de ce
théorème. Ce théorème est apparu en 1825 et
c'est en 1911 que le nom Napoléon lui est attaché. On rapporte que
Napoléon aurait soumis ce théorème à Lagrange
et Laplace en 1797, et ce dernier lui
aurait dit: Mon Général, nous nous attendions à tout de vous, sauf à des
leçons de géométrie. Laplace devint son ingénieur militaire en chef. |
|
|
|||
|
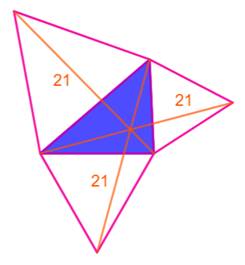
Propriétés Un triangle quelconque (bleu). Les trois triangles équilatéraux externes sur les
côtés. Les segments joignant un sommet
"équilatéral" au sommet opposé du triangle quelconque sont de même
longueur (ici 21). Le triangle (vert) dont les sommets sont les
centres des triangles équilatéraux est un triangle équilatéral. |
|
||
|
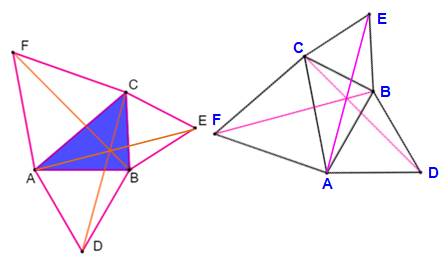
Démonstration de la première propriété Procéder à une rotation positive de 60° autour du
point A. Le point D vient sur B Le point C vient sur F Alors, DC = BF. Même chose pour AE =BF. |
|
||
Voir Brève
737
|
|
|||
|
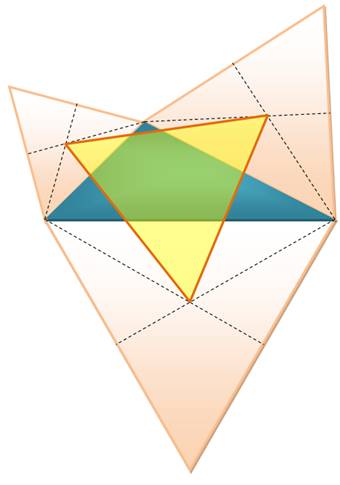
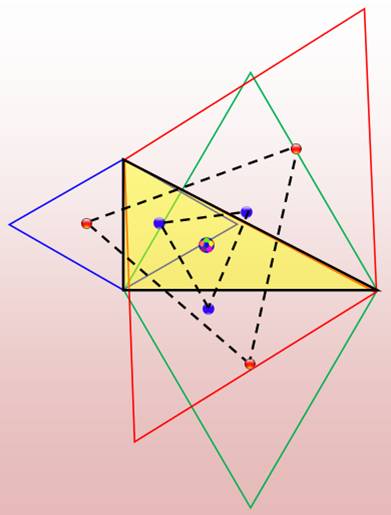
Construction externe Un
triangle quelconque (bleu). Les trois
triangles équilatéraux (roses) construits sur chacun des côtés, vers l'extérieur. Leur centre de gravité
(intersection des pointillés). Le
triangle (jaune) dont les sommets sont ces trois centres de gravité est
équilatéral. Théorème Dans un triangle quelconque, on relie les centres de gravité
des trois triangles équilatéraux construits sur les côtés et pointant à
l'extérieur. Le triangle obtenu est équilatéral. Condition Les
angles du triangle sont tous différents. |
|
||
|
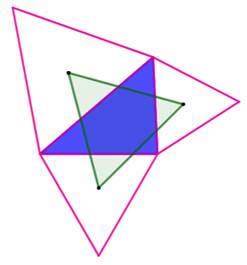
Construction interne et relations Le
théorème s'applique également pour les triangles équilatéraux construits en interne. Il existe
donc deux triangles équilatéraux Napoléon (pointillés). Leur
centre de gravité (G) est identique et c'est le centre de gravité du triangle
original. C'est le point Napoléon externe, noté X(17) dans l'encyclopédie
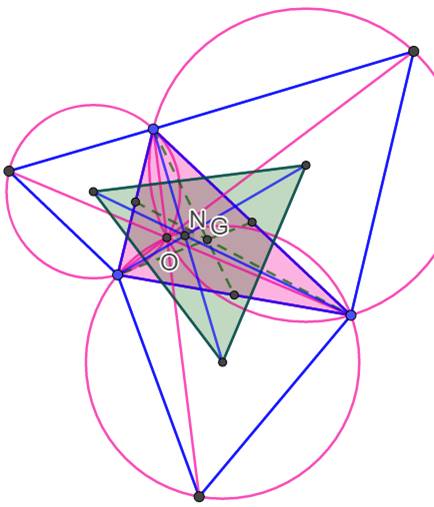
Kimberling Premier point de Fermat Voir figure ci-dessous à droite Les droites joignant un sommet du triangle Napoléon (vert) à un sommet
éloigné du triangle original (rose) sont concourantes en O et égales
(isométriques). Point
de Fermat. Le point de concours O est aussi le point de concours des trois cercles circonscrits aux triangles
équilatéraux. |
|
||
|
Second point de Fermat Le pendant du premier mais avec les triangles équilatéraux construits
vers l'intérieur. Aire du triangle externe
Aire du triangle interne
Ainsi la différence entre les aires des triangles Napoléon est égale à
l'aire du triangle initial. Point de concours (N) des droites qui rejoignent les sommets du
triangle initial aux centres de gravité des triangles équilatéraux. Notés X(17) et X18) dans l'encyclopédie
Kimberling. |
|
||
Voir Napoléon
|
|
||||
|
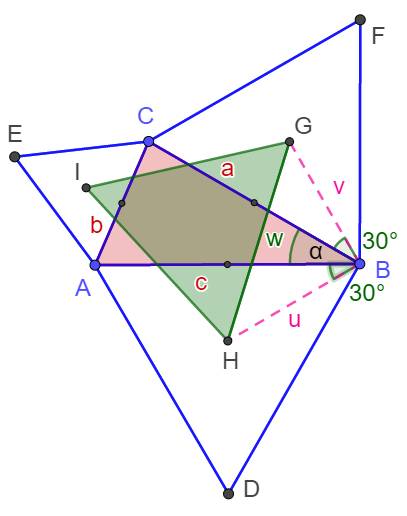
Les côtés
du triangle ABC mesurent a, b et c. On
s'intéresse au sommet B. L'angle
HBG est donc égal à
Restons
sur le segment BG, une portion de la médiane
du triangle équilatéral BCF. Sa mesure est connue:
|
|
|||
|
On va
maintenant résoudre le triangle BHG en invoquant la loi
des cosinus. |
|
|||
|
|
||||
|
En
substituant |
|
|||
|
Loi des
cosinus dans ABC |
|
|||
|
Loi
des sinus pour l'aire S du triangle ABC |
|
|||
|
Retour à
l'évaluation de w |
|
|||
|
Conclusion |
Cette évaluation est indépendante de l'ordre dans lequel on prend les
côtés a, b et c. En calculant la mesure des deux autres côtés du triangle Napoléon, on
trouverait cette même valeur. Le triangle Napoléon est bien équilatéral. |
|||
|
|
|||
|
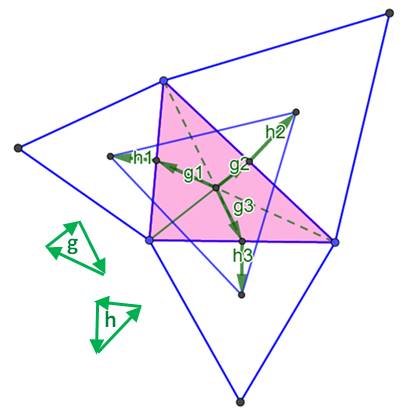
On
dessine les vecteurs
en g issu du centre
de gravité du triangle initial (on dit aussi: l'isobarycentre). Les
vecteurs en h sont issus du point milieu des côtés pour rejoindre le centre
de gravité de chaque triangle équilatéral. Propriété
du triangle équilatéral: les vecteurs en g ont mêmes mesures (un tiers de la médiane).
Ils sont orientés à 120° les uns des autres. Leur somme est nulle.
|
|
||
|
Dans le triangle de base, les vecteurs-côtés ont
une somme nulle. |
|
||
|
Mis bout à bout les vecteurs en h forment un
triangle semblable au triangle initial (Chacun est perpendiculaire aux côtés)
|
|
||
|
Le vecteurs entre centres de gravité sont somme
des vecteurs en g et des vecteurs en h. |
|
||
|
Cette relation montre que le centre de gravité du
triangle initial est aussi celui du triangle formé par les centres de
gravités des trois triangles équilatéraux. Elle ne signifie par que le nouveau triangle est
équilatéral. Il faudrait montrer que les normes (longueur) des vecteurs sont
égales. Voir ci-dessus |
|
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/Napoleon.htm
|
![]()