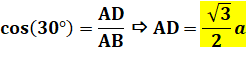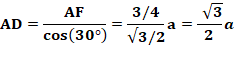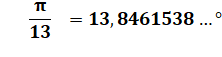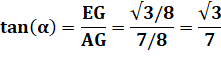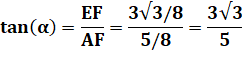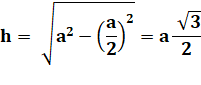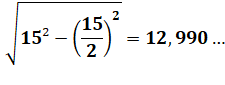|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
TRIANGLE ÉQUILATÉRAL (2/3) Propriétés générales en première partie. Propriétés spécifiques en
deuxième partie. Théorème de Viviani en troisième partie. |
|
|
||
|
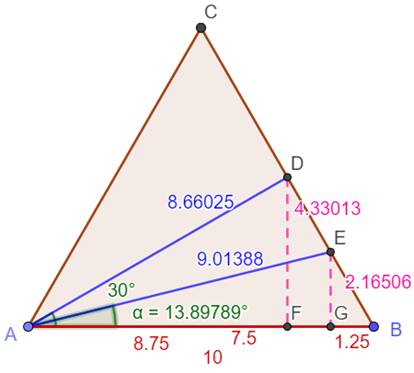
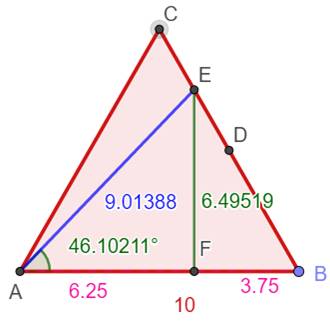
Triangle équilatéral ABC, D milieu de BC et E
milieu de BD. Quelle est la longueur de la médiane AD et celle
de la semi- médiane AE ? Médiane AD avec
AB = a = 10 Calcul direct
Calcul
indirect (utile pour ci-dessous) BF = 1/2 a cos60 = 10 x 1/4 = 2,5 AF = 10 x 3/4 = 7,5
|
|
|
|
Propriété remarquable avec AE
|
Calcul avec
AB = a = 10 BG = 1/4 a cos60 = 1/8 = 1,25 AG = 7/8 a = 8,75 EG = 1/4 a sin60 = a (racine de 3)/8 = 2,16…
|
|
|
Deuxième semi-médiane BF = 3/4 a cos60 = 3/8 = 3,75 AG = 5/8 a = 6,25 EF = 3/4 a sin60 = 3a (racine de 3)/8 = 6,49…
Fractions proches 10Pi/39 = 46,1538461… 257Pi/980 = 46,1020408… |
|
|
Voir Médianes du carré / Diagonales
des polygones
|
|
||
|
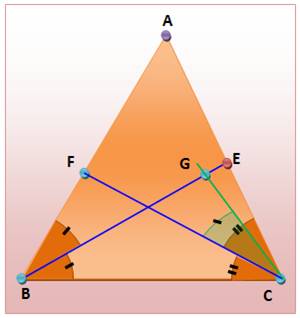
Théorème Tout
triangle ayant deux bissectrices d’égale longueur est isocèle. Historique En
1840, C.-L. Lehmus demande au géomètre suisse J. Steiner la démonstration de cette
propriété. Il a fallu plus d’un siècle pour simplifier la démonstration
compliquée de Steiner. La
plus simple, sans doute, est celle citée par Coxeter et Greitzer (Redécouvrons la géométrie) Démonstration On
va montrer le lemme suivant : au plus petit angle correspond la
bissectrice intérieure la plus longue. Alors : Or,
BE = CF, c’est que |
Les points bleus sur le même cercle On trace FCG, un angle égal
à BCFG (points bleus) sont
cocycliques car les angles égaux FBG et FCG interceptent le même arc FG. |
|
|
Démonstration du lemme
Or, si dans un cercle, deux cordes
sous-tendent des arcs correspondants à des angles inscrits égaux, au plus
petit angle correspond la plus grande corde. En effet, la corde la plus
courte est la plus éloignée du centre du cercle ; elle correspond donc à
un angle au centre plus petit et donc à un angle inscrit (sa moitié) plus
petit. Donc : au plus petit angle correspond la
bissectrice intérieure la plus longue. |
||
|
|
||
|
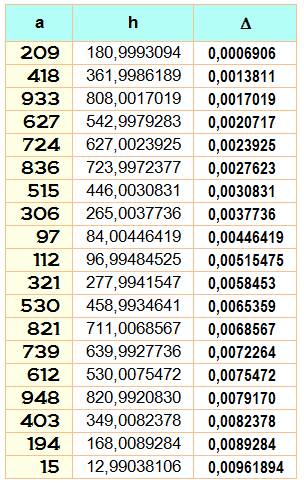
Hauteur
Cette valeur est presque entière lorsque a.racine
de 3 sur 2 est une valeur presque entière Exemple
|
|
|
|
|
||
|
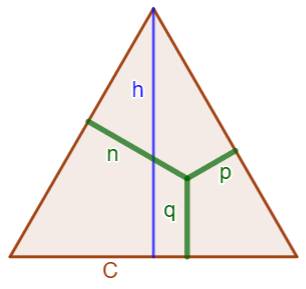
Théorème Dans un triangle équilatéral, la
somme des distances d'un point intérieur quelconque aux côtés est égale à la
longueur de la hauteur.
Cette
propriété se retrouve pour tous les polygones réguliers: Dans un polygone régulier, la somme
des distances d'un point intérieur quelconque aux côtés, est constante; c'est
celle obtenue en plaçant le point au centre du cercle inscrit. |
|
|
Voir Développements et application du théorème de Viviani / Brève 55-1093
|
|
||
|
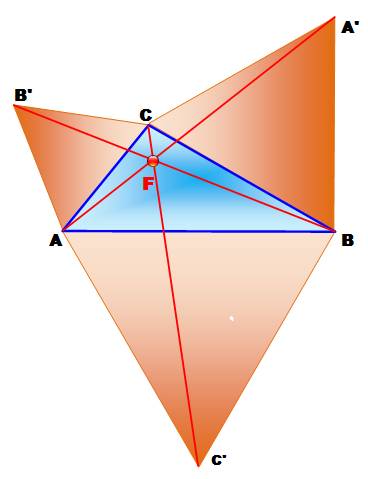
Un triangle quelconque ABC. Les trois
triangles équilatéraux posés sur chacun des côtés. Les trois
droites montrées se coupent en un point unique F, le point
de Fermat. Le point
F est tel que la somme des distances d'un point quelconque intérieur aux
côtés du triangle quelconque est minimum. Si à un
sommet, le triangle présente un angle de 120° ou plus, le point F coïncide
avec ce sommet. Défi posé en 1629 par Fermat à Torricelli. Ce
point se nomme aussi point de Steiner ou point de Torricelli. C'est le premier centre
isogonique du triangle. |
|
|
Voir Points remarquables du triangle / Points Napoléon
|
|
||
|
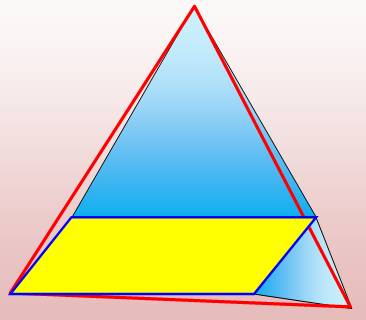
Un parallélogramme en jaune.
Deux triangles équilatéraux en bleu sur les côtés. Le
triangle en rouge est équilatéral. Les trois
petits triangles sur les bords sont égaux. Ce qui explique la propriété. |
|
|
|
|
||
|
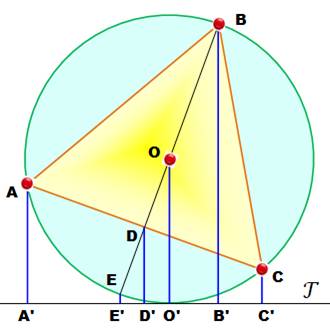
Un
triangle équilatéral ABC inscrit
dans un cercle.
Une tangente
quelconque. Théorème La somme
des distances des sommets à la tangente est égale à trois fois celle du
centre et à deux fois celle de la médiane
du triangle. AA' + BB' + CC' = 3 OO' = 2 BD Démonstration Elle
repose sur le fait que D est le milieu de AC; O celui de BE et D celui de OE. Pour le
dernier cas, on montre facilement que le quadrilatère AOCE est un losange;
les diagonales se coupent en leur milieu. La médiane BD
mesure 3/2 du rayon R = OB. (les médianes se coupent en O, lequel est
situé au deux tiers de la longueur de
la médiane. |
2DD'
= AA' + CC' 2OO'
= EE' + BB' 2DD'
= EE' + OO' AA'
+ BB' + CC' = 2DD' + 2OO' – EE' =
2DD' + 2OO' – (2DD' – OO') = 3 OO' = 3 R = 3 x 2/3 BD = 2 BD |
|
![]()
|
Retour |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TrgequiP.htm
|
![]()