|
||||||||||||||||||||||||||||||||||||||||||
![]()
|
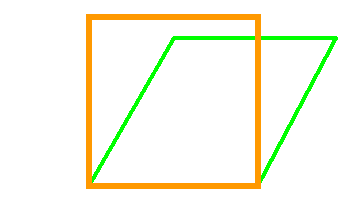
CARRÉ
RIGIDE Problème dont l |
|
|
||
|
Il n'est pas possible
de le déformer sans changer la longueur de ses côtés. |
|
|
|
Sans le casser. Simplement en faisant pivoter
les tiges sur leurs extrémités. |
|
|
|
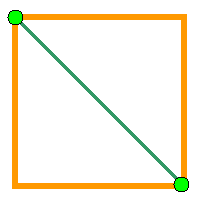
auquel cas on forme des
triangles, indéformables comme on
vient de le remarquer ci-dessus.
la tige diagonale
ajoutée a une longueur plus grande que celle des côtés du carré! |
|
|
|
|
||
|
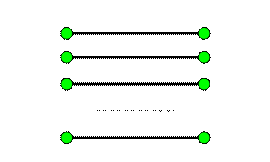
Problème
celle du côté du
carré (a).
La solution va
vous épater par la quantité stupéfiante nécessaire. |
|
|
|
Solution
Il faut en effet
23 tiges = 2 x 11 + 1
|
|
|
|
|
||
|
|
|
|
|
|
||||||||||
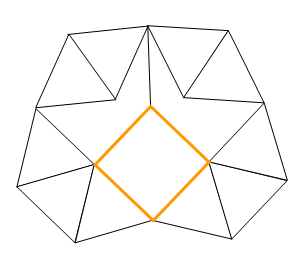
Ce problème appliqué ici
au carré est généralisable aux autres polygones réguliers |
||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()