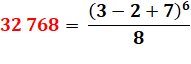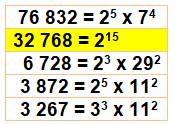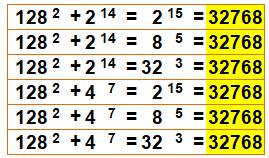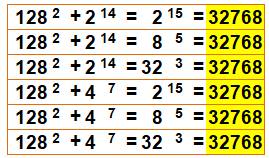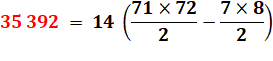NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/11/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres	DicoNombre NOMBRES				Glossaire Nombres
1 10 100 1000 5000 10 000 11 000 15 000 20 000	30 000 à 39 999				40 000 50 000 100 000 10^6 10^9 10^100
	Trente mille Anglais: Thirty thousand
30 000		32 000	35 000	37 000

30 000

30 007 = 2^2 + 3^2 + 5^2 + 7^2 + … + 71^2	Somme des carrés de vingt premiers consécutifs.
30 030 = 2 x 3 x 5 … x 13	Primorielle 13: produit de tous les nombres premiers jusqu'à 13.
30 031 = 59 x 509 = 2x3x5x7x11x13 + 1	Le plus petit nombre composé d'Euclide. Exemple de nombre utilisé dans la preuve de l'existence d'une infinité de nombres premiers.

Social	30 000 jours, correspond à environ 82 ans.	Jour
Astronomie	30 000 ans: traversée solaire de la lumière	Soleil
Géographie	30 000° dans un éclair. La température de l'air y est portée à 30 000°	Tonnerre
Informatique	30 000 foyers américains équivalent Sept 2023 Le chatbot d’OpenAI, ChatGPT, consommerait quotidiennement une quantité d’électricité équivalente à la consommation d’environ 30 000 foyers américains.	IA
Transport	30 000 ronds-points en France en 2015 Record du monde du plus grand nombre de carrefours. Près de la moitié de tous les carrefours giratoires du monde.	France
Langue	30 000 mots connus par un adulte français cultivé. 6 000 par un enfant de 11 ans. 270 000 dans le Trésor informatisé de la langue française.	Quantité de mots

30203 30203 903020309 3790302030973 98379030203097389 Etc.	Nombre premier palindrome qui reste premier en effaçant les deux chiffres de chaque côté. Il reste premier en lui ajoutant d'autres doublets de chiffres. Configuration pyramidale.
30 240 = 10! / 5!	Nombre quadri-factorielle (de la forme 2n! / n!), comme: 12, 120, 1680, 30240, … OEIS A001813
30 240 = 2^5 × 3^3 × 5 × 7	Nombre 4-parfait: somme des diviseurs = 120 960 = 4 × 30 240.
30 240 = 2^5 × 3^3 × 5 × 7 40 320 = 2^7 × 3^2 × 5 × 7	Deux nombres avec même chiffres et mêmes facteurs. Chacun possède 96 diviseurs dont 76 en commun (en rouge): 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 27, 28, 30, 32, 35, 36, 40, 42, 45, 48, 54, 56, 60, 63, 64, 70, 72, 80, 84, 90, 96, 105, 108, 112, 120, 126, 128, 135, 140, 144, 160, 168, 180, 189, 192, 210, 216, 224, 240, 252, 270, 280, 288, 315, 320, 336, 360, 378, 384, 420, 432, 448, 480, 504, 540, 560, 576, 630, 640, 672, 720, 756, 840, 864, 896, 945, 960, 1008, 1080, 1120, 1152, 1260, 1344, 1440, 1512, 1680, 1890, 1920, 2016, 2160, 2240, 2520, 2688, 2880, 3024, 3360, 3780, 4032, 4320, 4480, 5040, 5760, 6048, 6720, 7560, 8064, 10080, 13440, 15120, 20160, 30240, 40320. Voir Brève 56-1112

30 384² = 923 187 456	Le plus grand carré pannumérique.
30 694	Nombre méandrique.
	Différence minime entre les parties décimales des racines carrée et cubique

Préhistoire	31 000 ans Peintures de la grotte Chauvet. Les plus anciennes peintures rupestres connues.	Homo Sapiens
	31 337 => ELITE: remplacement des chiffres par des lettres, codage leet	Numéronyme

31 000

31 249^2 = 976 500 001	Puissance entière terminée par 00001.
31 333^7 = 29 649 259 480 984 782 858 578 077 020 877	Aucun chiffre en commun dans le nombre et sa puissance 7. Record.
31 623² = 1 000 014 129	Plus petit carré à dix chiffres.
31 623^3 = 31 623 446 801 367	Nombre qui se retrouve en tête dans son cube.

32 000

Biologie	32 000 ans depuis que l'homme est sur la Terre. Il a fallu 100 millions d'années de vie des bactéries pour préparer son arrivée.
Histoire	32 200 km de tranchées creusées durant la première guerre mondiale. Presque le tour de la Terre (40 000 km).	>>>

32 043 ² = 1 026 753 849 99 066 ^2= 9 814 072 356	Carrés donnant un nombre pannumérique (avec 0). Le plus petit et le plus grand.
32323 323232323 32323232323	Nombres premiers ondulants en 2 et 3. Le suivant a plus de 2000 chiffres.
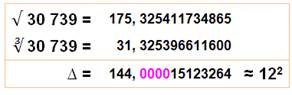
32 592,000046…	Multiple proche d'un entier.
32 761 = 181² = 2^15 – 7	Plus grand carré de la forme 2^p – 7.

Forme des carrés

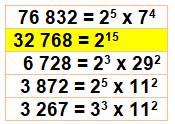
32 761 = 105^3 – 104^3 = (9² + 10²)²		Avec nombres successifs des deux côtés.
32 768 = 32^3 = 8^5 = 2^15		Puissance. Opération avec ses chiffres (Edmark M.Law).
		Puissances avec les chiffres de 2^15.
		Carré + puissance = puissance. Plusieurs façons d'exprimer la même somme (exemple): 16 384 + 16 384 = 327 768 = 2^15
32 907 + 65 814 + 98 721	Somme a + 2a + 3a qui présentent dix chiffres différents. Le plus grand motif avec termes de cinq chiffres.
32 993 = 2^15 + 15^2	Nombre premier de Leyland (3^e).

33 000

33 075 = 15^3 + 16^3 + … + 20^3 = 11^3 + 12^3 + … + 19^3	Somme de cubes consécutifs deux fois.
33 124 = 182²	Plus petit carré avec les quatre premiers chiffres. 135 424 = 368² est le suivant avec les cinq chiffres (1, 2, 3, 4, 5).
33 280 = 8^3 + 32^3 = 832 (8 + 32)	Somme de deux cubes avec coquetterie.
33 335² = 1 111 222 225	Curiosité.
33 461	Nombre de Pell
33 518² = 1 123 456 324	Curiosité: plus petit carré ayant six chiffres successifs.
33 600 = 25 920 + 7 680	Nombre égal au produit des factorielles de ses chiffres ajouté à la quantité de nombres premiers plus petit que lui. Liste: 11, 40, 101, 432, 2016, 10111, 33600, 101111, 1011001, 1100101…
33 614 = 2 x 7^5 33 615 = 3^4 x 5 x 83 33 616 = 2^4 x 11x 191	Trois nombres successifs avec des cubes.
33 744 = 2^4 x 3 x 19 x 37 33 744 n^36 - 1 Si n premier avec 2, 3, 19 et 37	Divisibilité Exemple: 5^36 - 1 = 14 551 915 228 366 851 806 640 624 = 33 744 x 431 244 524 311 488 021 771

34 000

34 425 = 3^4 x 425 344 250 = 3^4 x 4250 3 442 500 = 3^4 x 42500 …	Nombre de Friedman. Motif infini, comme avec 312 325. Nombre faute de frappe.
34 560 = 1! x 2! x 3! x 4! x 5!	Superfactorielle (ou factorielle géante): produit des cinq premières factorielles. Voir Nombre 3 456
34 560 = 1^5 ∙ 2^4 ∙ 3^3 ∙ 4^2 ∙ 5^1 = 2^8 ∙ 3^3 ∙ 5	Nombre PNCPCI: puissances consécutives de nombres consécutifs. Notez les chiffres consécutifs dans le nombre.
34 560 divise (f-a)(e-a)(d-a) …	Le PGCD des produits des différences entre six nombres est 34 560.
34 879 = AUTOS = ROLLS + ROYCE	Puzzles numériques
34 969 = 187² = (11 × 17)² 34 969 = 187² = (14² – 3²)² 34 969 = 187² = (94² – 93²)²	Mentionné dans Sesame Street 187 est le code américain de la police. Note:

Géographie	34 000 m Largeur minimale de la Manche. La manche mesure 500 km de long et entre 250 et 34 km de large au détroit de Douvres.	>>>
	34 955 communes au 1^er janvier 2022 en France. 34 826 en métropole et 129 en départements et régions d'outre-mer, Mayotte comprise.	>>>
Multimédia	34 969 nombre favori de Count von Count (parodie du conte Dracula) dans Sesame Street. Pourquoi ce nombre ? Voir ce nombre ci-dessus. Il a aussi mentionné le nombre 6 523 728 en indiquant que ce serait son âge en octobre 2017.

35 000

Préhistoire	35 000 ans – Période de bascule. Avant l'homme de Neandertal occupait toute l'Europe. Après, l'Homo Sapiens l'a remplacé.	>>>
Vie	35 000 grains de riz dans un kilogramme. Riz thaï: 50 000; Basmati: 65 000.

60 = 2^2 × 3 × 5 2235 = 3 × 5 × 149 35 149 Fin, car premier	Exemple d'un premier d'une itération de Conway nommée "Climb to a prime". Sa conjecture disant que tout nombre finit par un premier a été infirmée par ce contre-exemple: 13 532 385 396 179 = 13 × 53^2 × 3853 × 96179 qui se réplique lui-même. Trouvé par James Davis. On ne sait pas encore si le nombre 20 s'arrête.
35 336 = 2^2 + 3^2 + 5^2 + 7^2 + … + 73^2	Somme des carrés de 21 premiers consécutifs.
353 35353	Nombres premiers ondulants en 2 et 5. Le suivant a 23 chiffres.
	Somme des nombres de 100 à 1000 divisibles. par 14. Calcul Somme de 112 (le premier divisible par 14) à 994, le dernier. Chacun est un multiple de 14: soit la somme de tous les nombres de 8 à 71 fois 14.
35 641^4 = 1 613 613 516 634 136 161		Plus petite puissance 4 ayant les mêmes chiffres que son nombre.

35 890	Nombre tribonacci.
35 899 = 8! – 7! + 6! – 5! + 4! – 3! + 2! – 1!	Factorielle alternée.
35 937 = 33^5 + 7 – 9 = 33^3	Anagrammes numériques. Nombre de Friedman.

Langue	Trente six mille solutions	Expressions
Multimédia Astronomie	36 000 km Altitude des orbites des satellites de communication. À cette altitude, un satellite tourne autour de la Terre en 24h: orbite géostationnaire. Voilà qui explique pourquoi votre parabole est toujours bien pointée sur le satellite. Les stations spatiales se trouvent, elles, à partir de 200 km.	>>>

Il n'arrivait pas à s'habituer aux conversations par satellite. Penser que le signal devait monter jusqu'à des trente-six mille kilomètres et redescendre par la même voie … pas étonnant qu'il y ait des arrêts et des chevauchements.

Extrait d'Abysses / Voir Pensées & humour

36 000

36 000 = (1×10)^3 + (2×10)^3 + (3×10)^3	Somme de cube dans le ratio1, 2 et 3. Liste: 36, 288, 972, 2304, 4500, 7776, 12348, 18432, 26244, 36000, 47916, 62208, 79092, 98784, 121500, 147456, 176868, 209952, 246924, 288000, …
36 361² = 1 322 122 321 363 639² = 132 233 322 321	Carré avec chiffres 1, 2 et 3. Le suivant. Notez la forme semblable.

37 000

37 037 = 7 . 11 . 13 . 37 37 037 x 3 = 111 111 37 037 x 3 x 8 = 888 888	Multipliez 37 037 par a, un chiffre de 1 à 9, puis par 3. Résultat: le repdigit aaa aaa.
37 338 partitions de 40	Toutes les partitions.
37 373	Nombre premier ondulant en 3 et 7. Le suivant a 21 chiffres.
37 378	Semi-méandrique.
37 811 & 37 813	Nombres premiers consécutifs ou jumeaux.
37 960 = 2^3 x 5 x 13 x 73 37 961 = 7 x 11 x 17 x 29 37 962 = 2 x 3^3 x 19 x 37	Premier triplet de nombres consécutifs ayant quatre facteurs non répétés.
38 227	Nombre de Genocchi.
38 416 = 196^2 = 14^4	Puissance.

Cosmologie	38 888 m/s Vitesse de l'engin spatial le plus rapide en 2013.	>>>
Nombre	38 889 chiffres pour compter de 0 à 9 999.	>>>
Géographie	39 300 km Estimation du tour de la Terre par Ératosthène.	>>>
Social	39 340 euros Dette publique française en 2020 par habitant. 14 380 euros en 2000. 26 309 euros en 2010.

39 304 = 34^3 = 102² + 170² = 10² + 198²	Cube somme de deux carrés.
39 338 = 163² = 23² + 197² = 97² + 173² = 107² + 167² = 113²	Nombre carré quatre fois somme de deux premiers.
39 999 = 4 x 10^4 – 1 = 3 x 67 x 199	Certains nombres de cette forme sont premiers; pas ceux avec n = 1 mod 3.

Suite	Nombres 40 000
Voir	Nombre Chanceux Semaine Palindrome Triangle Tectroèdre Raisonnement Rep Unit Suites Nombre Têtus
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N30000.htm

Archives

Coût de possession des PC en 1998 >>>