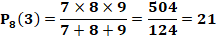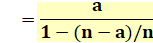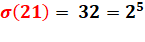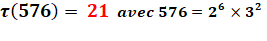nombre vint et un en maths

Édition du: 29/12/2024

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10⁶ / 10⁹ / 10¹⁰⁰ / Infini
	-0-	10		20	30		40	50	60	70	80	90
	20	21		22	23		24	25	26	27	28	29

Nombre 21

Maths générales du 21

Maths détaillées du 21

Vingt-et-un

Twenty-one

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 0101
Bases	111₄ 33₆
Romain	XX I

Suite

Préfixes diviseurs et multiplicateurs:

10^-21 zepto

10²¹ zêta

Plus petit nombre dont la somme des diviseurs est une puissance 5. Suivants: 31, 651, 889 …

Caractérisation du nombre

2-hyperparfait

Blum (facteurs = 3 mod 4)

Brillant

Chanceux d'Ulam

Coefficient du binôme

Composé

Composé inévitable (ou minimal)

Congruent

Curzon

Déficient

Dihédral

D-nombre

Docile (amenable)

Facteur carré (sans)

Fibonacci (8^e)

Harshad

Hyperparfait (ordre 2)

Idonéal

Impair

Interpremier (19, 21, 23)

Jacobsthal (6^e)

Mian-Chowla

Motzkin (5^e)

Narcissique de Keith

Narcissique généralisé

Padovan

Pratique

Semi-premier

Simple

Stirling 1 (1^ère et 2^e espèces)

Touchable (hautement)

Hogben (5^e)

Octogonal (3^e)

Palindrome en binaire

Pascal

Triangulaire (6^e)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

Chiffres – Numération

21₁₀ = 12₁₉		Exactement les mêmes chiffres en base 19.
21₁₀ = 210₃		Ressemblance en base 3.
21 + 12 = 33 21 × 12 = 252		Devient repdigit lorsqu'ajouté à son retourné et palindrome en le multipliant.
21 = 2+1 + 9+2+6+1 21³ = 9 261 21 = 2+1 + 4+0+8+4+1+0+1 21⁵ = 4 084 101		Narcissique de Keith Somme de ses chiffres et de ceux de son cube. Somme de ses chiffres et de ceux de sa puissance 5. Voir Table des nombres de Keith
21 => 2³ = 8, 1³ = 1 => 81 = 9²		Nombre dont les chiffres mis au cube puis concaténés produit un carré.
21 = 7 x (2 + 1) & 12 = 4 x (1 + 2) 42 = 7 x (4 + 2) & 24 = 4 x (2 + 4) 63 = 7 x (6 + 3) & 36 = 4 x (3 + 6) 84 = 7 x (8 + 4) et 48 = 4 x (4 + 8)		Un des quatre nombres sept fois somme de ses chiffres. Motif inverse pour quatre fois la somme
21 = (2²x1²) + (2⁴+1⁴) 21 = (2⁴x1⁴) + (2²+1²) 21 = (4x4x1) + (2²+1²) Avec 21² = 441		Nombre somme-produit avec ses chiffres ou ceux de leurs puissances.
(2 + 1)² = 4 + 4 + 1	Le carré de la somme des chiffres est égal à la somme des chiffres du carré.
21 – 9 = 12	Plus petit nombre qui se retourne lorsqu'on lui retranche un nombre en 9.
12 = 3 + 4 + 5 21 = 6 + 7 + 8	Cinq chiffres consécutifs. Avec son inverse, on trouve 6 chiffres consécutifs.
21 = 6 x 3 + 3 = 63 / 3	Mêmes chiffres de part et d'autre de l'égalité.
21	Nombre chanceux d'Ulam (crible).
21 ≠ mn – m – n	Le plus petit nombre NON 2-McNugget: jamais de la forme mn – m – n quels que soient les nombres m et n. Liste: 21, 33, 45, 57, 61, 73, 75, 77, 81, 85, 87, 91, 93, 99, …

Addition

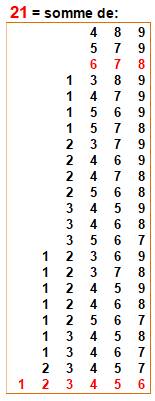
p(21) = 792	Quantité de partitions du nombre.
21 = 1 + 2 + 3 + 4 + 5 + 6 = 7 x 3 = 6 + 7 + 8	Somme des nombres successifs. Somme égale au triple du nombre suivant. Partition unique avec six chiffres différents. Somme des chiffres inscrits sur un dé à jouer.
21 = 1 + 2 + 3 + 4 + 5 + 6 21 et 15 sont triangulaires 21 – 15 = 6 et 21 + 15 = 36 aussi	6^e Nombre triangulaire. La plus petite paire avec cette propriété.
21 = 1 + 7 + 13 = 3 x 3² – 2 x 3	8^e Nombre de Fibonacci. 3^e Nombre octogonal.
21 = 2 + 2 + 17 = 3 + 5 + 13 = 3 + 7 + 11 = 5 + 5 + 11 = 7 + 7 + 7	Plus petit nombre cinq fois somme de trois nombres premiers.
21 = 2 + 19 = 3 + 5 + 13 = 3 + 7 + 11 = 2 + 3 + 5 + 11	Plus petit nombre somme de deux, trois et quatre nombres premiers.
21 = 1 + 3 + 4 + 7 + 6 21 = (1) + (1+2) + (1+3) + (1+2+4) + (1+5)		Cumul de la somme des diviseurs des 5 premiers nombres.

Multiplication – Division

21 = 3 x 7	Nombre simple Nombre composé. Produit de deux facteurs premiers. Qui représentent la Trinité et les jours de la création. Nombres produit de deux nombres premiers cousins.
21 / (2 + 1) = 7	Le plus petit des quatre 7-Harshad.
		Coefficient du binôme (nombre de Pascal) Quantité d'issues primitives avec deux dés. Choix de 2 parmi 7 ou 5 parmi 7.
		Motif avec factorielle tronquée.
		Division avec des factorielles.
		Exemples de fractions exprimant le nombre 21. Il en existe une infinité avec a quelconque. Forme valable pour 21 comme pour tout nombre n.

21 / 12 = 1,7 321 / 123 = 2,6 4321 / 1234 = 3,5 etc.	Division d'un nombre par son retourné. Les deux premiers chiffres significatifs du quotient: le premier vaut le premier chiffre de gauche moins 1, et le second est son complément à 8.
1+1+2+3+5+8+13+21+34+ 55+89+144+233+377+610+987 = 2583 = 21 x 123		La somme de 16 nombres de Fibonacci consécutif est divisible par 21.
		La somme des diviseurs est une puissance.
		Plus petit nombre dont la quantité de diviseurs est 21. Calcul: (6 + 1) (2 + 1) = 7 × 3
PGCD(21, 2k+1 < 21) = 1		Les 5 nombres impairs premiers avec 21 (5, 11, 13, 17, 19) sont effectivement premiers.
21 – 2^k avec k de 1 à 4 => 19, 17, 13, 5		Sont tous premiers.
21 [18, 51, 91]	Nombre hautement touchable. Le nombre 21 est la somme des diviseurs propres de ces 3 nombres (somme aliquote). Plus petite valeur pour trois sommes.

Puissance

21 = 1² + 2² + 4² = 2² + 2² + 2² + 3²	Seule somme de puissances de 2 à 5 avec deux à cinq termes (sans répétition de 1).
21 = 6² – 5² + 4² – 3² + 2² – 1²	Motif dont toutes les puissances paires sont divisibles par 7. Ici avec 2, la somme alternée vaut 21 qui est divisible par 7.
21 = 1¹ + 2¹ + 3¹ + 4¹ + 5¹ + 6¹ = 3 x 7	Somme de puissance de nombres consécutifs jusqu'à n, divisible par le nombre suivant (n + 1) quelle que soit la puissance. Propriété générale.
21 = 4 + 8 + 9 = 5 + 6 + 10 161 = 4² + 8² + 9² = 5² + 6² + 10²	Égalités valables pour les entiers comme pour les carrés. Suivre le lien pour voir les six égalités de ce genre pour 21.
21 = 2² + 2² + 2² + 3²	Somme des carrés de quatre nombres premiers.
21 = 5² – 5 + 1	Nombre polygonal centré d'ordre 2 ou nombre de Hogben.
21 = 4⁰ + 4¹ + 4²	Somme puissances de 4.
21 = 11² – 10² = 11 + 10 = 5² – 2²	Différence de deux carrés. Sous deux formes. 15 est le plus petit – le suivant est 21. Motif général.
21 = 11² – 10²	Début d'une série de répétitions de chiffres en 22…221.
21	Racine triangulaire de 6.

En Puissance

Infinité de triplets de Pythagore

Voir Nombre 99 / Autres formes de ce type

12² = 144 21² = 441	Motif qui marche aussi pour 13.
21² = 221² – 220² = 221 + 220	Triplet de Pythagore jumeau. Notez les seuls chiffres 0, 1et 2 et les deux carrés en 21.
21⁸ x 8 = 302 582 874 888	Super 8 nombre. Le plus petit en 8.
508 853 989² = 25 893 238 21 21 21 21 21 1 318 820 881 ² = 173 928 851 61 61 61 61 61	Si un carré se termine par xy xy xy xy xy alors xy vaut 21, 61 ou 84. Voici les deux plus petits avec ce motif.
2²¹ = 2097152 => 122579	Le nombre formé par les chiffres rangés par ordre croissant est un nombre premier.
3²¹ = 10460353203	Puissance de 3 qui commence par 10. Avec 3^k, ces puissances commencent par 10 pour: 21, 42, 65, 86, 109, 130, 174, 195, …

Dénombrement, jeux et curiosités

		Jeu du quatre 4.
21		Quantité de nombres premiers à deux chiffres.
Il faut 21 carrés élémentaires…		Pour disséquer en carrés distincts. Le plus petit carré possible. La longueur de son côté est 112.
21	Nombre busy beaver (castor affairé) d'ordre 3.
21	Nœuds premiers possédant huit croissements dans l'espace (ℝ³).
21	Carrés élémentaires constituent le carré parfait de côté 112.
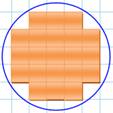
21	La quantité maximale de carrés unités alignés inclus dans un cercle de rayon 3 est 21. Résoudre le cas général pour un rayon R donné est connu comme le problème de Gauss.