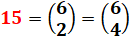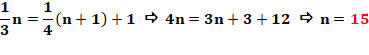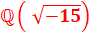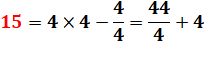|
Édition du: 03/03/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
|||||
Préfixes
diviseurs et multiplicateurs: 10-15 femto 10 15 péta (É-U: quadrillion) |
||||||
|
Caractérisation
du nombre
|
|
Voir |
||||
Rappel
Propriétés générales >>>
Numération,
chiffres, dénombrement
|
15 + 51 = 66 = T11 51 – 15 = 36 = T8 |
|
|||
|
15 = 11112 = 334 = 1114 15 = 24 – 1 = 23 + 22 + 2 +
1 = 11112 |
|
|||
|
15 =
3 × 5 51 = 3 ×
17 |
|
|||
|
15 => 1² = 1, 5² = 25
=> 125 = 53 |
|
|||
|
15
= 1 + 5 + 2 + 2 + 5 |
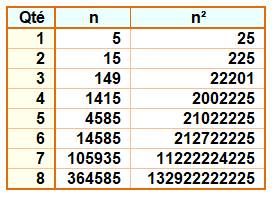
Somme de ses chiffres et de ceux de son
carré. |
|||
|
15 =
3 x 5 |
Un
polygone à 15 côté est constructible
à la règle et au compas. |
|||
|
15 = (1x5) x 3 |
|
|||
|
15 = 3 + 3·2 + 3·2·1 {1, 2, 3, 12, 13, 21, 23, 31, 32, 123, 132, 213, 231, 312, 321} |
|
|||
|
15, 46, 23, 70, 35,
106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4,
2, 1 |
|
|||
|
15 = C62
= C64
|
Combinaisons
de 6 objets pris 2 par 2 ou 4 par 4. Deux
notations possibles; la seconde est préférable. |
|||
|
15 |
246×320×59×76×112×133×17×19×23×29×31×41×47×59×71
= 808 0174247945 1287588645 9904961710 7570057543 68000000000 = 8,08… 1053. |
|||
|
15 |
|
|||
Partitions - Additions et soustractions
Il
existe 176 partitions du nombre 15.
Avec
les nombres de 1 à 4, par exemple, il y
a Qp = 54 partitions
dont
dQp = 27 en plus par rapport aux nombres de 1 à 3

Les 176
partitions de 15
Voir Partitions du nombre 5 – Diagramme de Ferrers / Quantité
de partitions
Théorème des 15
|
Si une forme quadratique définie positive, dont
la matrice est à coefficients entiers, représente les nombres {1, 2, 3, 5, 6,
7, 10, 14, 15}, alors, elle représente tous
les entiers positifs. Voir Formes
quadratiques et ce théorème |
|
|
|
|
|
15 = 1 + 2 + 3
+ 4 + 5 27 = 2
+ 3 + 4 + 5 + 6 + 7 429 = 4 + 5 + … + 28 + 29 |
Nombres
étonnants: somme qui reprend ses chiffres pour les extrêmes. Voir Nombre 429 |
|
|
15 = 1 + 2 + 3 + 4 + 5 21 et 15 sont triangulaires 21 – 15 = 6 et 21 + 15 = 36 triangulaires aussi |
|
|
|
15 + 21 = 36 21 – 15 =
6 |
|
|
|
15 = 1 + 2 + 3 + 4 +
5
= 4 + 5 + 6
=
7 + 8 |
|
|
|
15 = 4 + 5 + 6 = 7 + 8 |
|
|
|
15 = 6 + 5 + 4 = 3 x 5 |
|
|
|
15 = 3 + 5 + 7 |
|
|
|
15 = 2 + 2 +
11 = 3 + 5 + 7 = 5 + 5 + 5 |
|
|
|
15 = 1 + 2 + 4 + 8 |
|
|
15 = 1 + 5 + 9
= 1 + 4 + 10 |
|
|
15 = (1 + 1) 5 + 5 |
|
|
15 = 1 + 2 + 3 + 4 + 5 30 = 6 + 7 + 8 + 9 |
|
|
15 = 1 + 3 + 4 + 7 |
|
|
15 = 2
+ 6 + 7 = 3
+ 4 + 8 89
= 2² + 6² + 7² = 3² + 4² + 8² 15 =
1 + 6 + 8 =
2 + 4 + 9 101 = 1² + 6² + 8² = 2² + 4² + 9² |
|
|
15 = P7 |
Voir Partition de 7 – Diagramme de Ferrers |
|
Question: quel est le nombre n tel que son tiers excède
le quart du nombre suivant d'une unité ? Réponse:
|
|
|
|
||
|
15 = 24 –
1 = (22 – 1) (22 + 1) = 3 x 5 |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
Liste: 1, 3, 15, 28, 255, 744, 2418,
20440, … OEIS A018784 |
||
|
PGCD(15,
2k+1 < 15) = 1 |
|
||
|
11 13 15 17
19 |
|
||
|
15 – 2k
avec k de 1 à 3
=> 13, 11, 7 |
|
||
|
|
Ce corps
contient tous les nombres de la forme a + ib |
||
Puissances
|
15 = 1² + 1² + 2² + 3² |
|
||
|
15 = 20 +
21 + 22 + 23
= 24 – 1 |
|
||
|
15 = 16 – 1 = 4² – 1
= 3 x 5 |
|
||
|
15 = 8² – 7² = 64 – 49
= 4² – 1² |
|
||
|
|
|||
|
15 = 43 –
7² =
64 – 49 |
Différence
entre un cube et un carré. |
||
|
15 = 26 –
7²
= 43 – 7²
= 82 – 7² |
|||
|
42 – 1 = 15 44 – 1 = 255 46 – 1 = 4095 48 – 1 = 65535 … |
|
||
|
15 et 16 |
|
Voir Pépites numériques |
|
|
15 = 5! / 23
= 120 / 8 |
|||
|
5² +
12² = 13² 15²
+ 112² = 113² |
Sans doute
unique. D'autres existent avec en-têtes différents. |
||
|
24n
– 1 est
divisible
par 15 |
24 – 1 = 15 28 – 1 = 255 = 15 x 17 212
– 1 = 4 95 = 15 x 273 |
||
|
1 + 2 + 3 + … + 15
= 120
= 5 x 4!
= 1 x 5! |
Avec
la somme des
nombres jusqu'à n: S = n (n + 1) /
2:
|
||
|
3n5
+ 5n3 + 7n est divisible
par 15 |
|
||
|
n5
– n = (n2 + n + 3) (n3 – n2
– 2n + 5) – 15 = (n2 – n + 3) (n3
+ n2 – 2n – 5) + 15 |
|
||
|
2331…21 x
101656521 = a(4) |
a(n) =
e^e^e…e n fois. |
||||
|
215 + 15 = 32 783 nombre premier |
|
||||
|
15² = 9² + 12² = 225
= 2² + 5² + 14²
= 2² + 10² + 11² |
|
||||
|
15² = 225 35² = 1225 45² = 2025 |
|
|
|||
|
154 = 24 + 24
+ 64 + 124 + 134 |
dont la 2e
avec nombres distincts et la 3e comme multiple de: 54 =
24 + 24 + 34 + 44 + 44 |
||||
|
154 = 2252 =
50 625
2552 = 65 025 |
|
||||
|
155 = 759 375 = (7 + 5 + 0 + 3 + 0 + 0)5 |
(Entrée faible ! Voir NESHIP) |
||||
|
1512
=
129 746 337 890 625 3112 = 787 662 783 788 549 761 |
Il faut atteindre 31 pour avoir tous
les chiffres sauf le "0". Ce nombre a 18 chiffres. |
||||
|
|
|
||||
Jeux
|
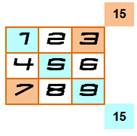
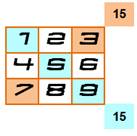
15 |
Voir La magie des sommes
des carrés. |
|
|
|
|
|
|
|
|
|
|
15 = 4! – !4
= 24 – 9 |
|
|
|
15 = 1/6 (43
+ 5x4 + 6) |
|
|
Décimales
|
15,15 … = 15,154262241479264189… |
Soit la
courbe réunissant les solutions non triviales de xy = yx.
La droite x = y la croise au point x = y = e et, à ce point, xy =
ee.
|
|
15,43… 15,438887358552... |
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2, [1, 1, 1, 1] 3, [1, 2, 0] 4, [3, 3] 5,
[3, 0] 6,
[2, 3] |
7,
[2, 1] 8,
[1, 7] 9,
[1, 6] 10,
[1, 5] 11,
[1, 4] |
12,
[1, 3] 13,
[1, 2] 14, [1, 1] 15,
[1, 0] |
2,
[1, 1, 1, 1] 4,
[3, 3] 14,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
![]()