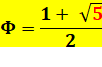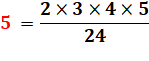|
Édition du: 01/03/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
|
Nombre 5 |
Culture 5 |
Maths
5 |
Expressions
en 5 |
|
|
Débutant
5 |
Culture 5 |
Opérations
avec 5 |
Jeux en 5 |
Proverbes
avec 5 |
|
Quizz
5 |
Sciences 5 |
Divisibilité
par 5 |
Homophones du
5 |
|
|
Nombre
d'or et 5 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
|||
|
Voir Partitions |
||||
|
|
|
Relation intime avec
Voir |
||
Rappel
Propriétés générales >>>
![]()
PROPRIÉTÉS MATHÉMATIQUES générales
|
|
||
|
Quel symbole placer entre ces deux nombres pour
obtenir un nombre plus grand que 5, mais plus petit que 6? |
||
|
Un pas vers la conjecture
faible de Goldbach: tout nombre impair supérieur ou égal à 9 est somme de
trois nombres premiers impairs. |
||
|
|
||
|
Pour multiplier par 5, ajoutez un zéro et divisez
par 2. Pour diviser par 5, décalez la virgule d'un cran
vers la gauche et multipliez par 2. |
||
|
Toutes les puissances de 5 se terminent par 5. |
||
|
Le produit de deux
nombres se terminant par 5 se termine lui-même par 5. Les multiples
de 5 se terminent par 0 ou 5. |
|
|
|
Le carré d'un nombre terminé par 5 se calcule très simplement. |
||
|
Autres
opérations avec 5. |
||
|
Motif valable pour tout nombre impair. |
||
|
|
||
|
(6, 8, 10), (5, 12, 13), (6, 25, 29), (7, 15, 20)
et (9, 10, 17) |
||
|
|
||
|
Seul polygone à avoir autant de côtés que de diagonales. |
||
|
Tétraèdre, Cube, Octaèdre, Dodécaèdre, Icosaèdre. |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
![]()
PROPRIÉTÉS
MATHÉMATIQUES détaillées
Chiffres et numération
|
5 |
|
|
|
|
Type
séquence
|
1 2 3 4 5 6
7 8 9 |
|
|
1, 1, 2, 3, 5,
8, 13 … |
|
|
1, 2, 5, 14,
42, 132 … |
|
|
1, 1, 2, 5,
15, 52 … |
|
|
1, 5, 61, 1
385 … |
|
|
5 et 1 645 333 507 |
Toutes les manières de faire 5 avec des additions
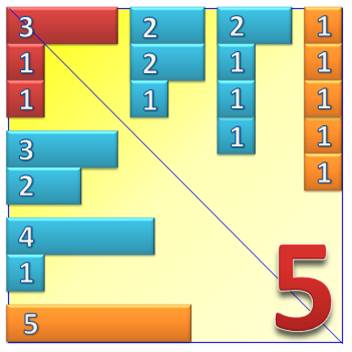
Voir Diagramme
de Ferrers / Partitions du nombre 15
(exemple)
Addition
|
5 = 3 + 2
=
3² – 2² |
|
|
5 = 3 + 2 et 3 x 2 =
6 |
|
|
5 +
1 = 7 – 1 (5 – 1) x 2 = 7 + 1 |
|
|
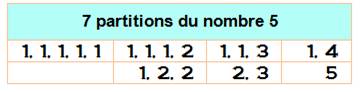
5 = 1 + 1 +
1 + 1 + 1
= 2 + 1 + 1 + 1
= 2 + 2 + 1
= 3 + 1 + 1
= 3 + 2
= 4 + 1
= 5 |
Le nombre 5 possède sept partitions: P(5) =
7. Voir Diagramme de Ferrers ci-dessus |
|
5 partitions
= (4) |
Partitions
du nombre 4. |
|
5 = 1x1! + 2x2! 5 = 3! – 2! + 1! |
|
|
5 + 1 + 9 = 15 5 + 2 + 8 = 15 … |
|
|
5 = –1 + 2 – 3 + 4 …
+ 10 |
|
|
55 = 8² – 3² … |
|
![]()
Table
de multiplication du 5

Voir Table
complète
|
5 = 1 x 5 |
|
|
5 = 1 x 61
– 1 |
|
|
5 = ½ (3 x 2² – 2) |
|
|
5 = 3! – 1 = 1 x 2 x
3 – 1 |
|
|
5 |
|
|
2 × 3 × 5 – 1 premier |
|
|
5 ≠ 2a٠3b
|
|
Voir Diagramme
de Hasse des nombres multiples de 2, 3 et 5
|
|
|
||
|
5 = 2 + 3 = 7 – 2 |
|
||
|
5 | (2 + 3) |
|
||
|
5 |
|
||
|
|
|
||
|
|
|
||
|
n / 5 = 2n / 10 |
|
||
|
k | (n² + 1) &
(n + 1)² + 1 |
|
||
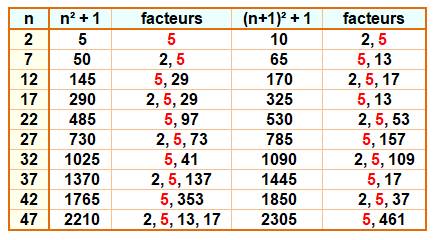
Voir Brève 47-932 / Nombre
13 / Nombre
29 / Nombre
61
|
5 = 6! / 12² = 720 /
144 =
6! / (3! x 3! x 2²) |
||
|
4n – 3n + 2n – 1n |
|
|
|
|
||
|
N'est jamais somme des diviseurs
d'un nombre. |
|
|
|
5 & 2 x 5 + 1 =
11 sont
premiers 2 & 2 x 2 + 1 = 5 sont
premiers |
|
|
|
|
Forme
valable pour 5 comme pour tout nombre n. |
|
|
|
Ce corps
contient tous les nombres de la forme a + ib |
|
![]()
Autour du nombre
|
5 = Qe(4) |
|
|
|
|
||
|
5 |
|
|
|
5 |
|
|
|
5 |
|
|
|
25
– 1 = 31 = M5 |
|
|
|
5! + 1 = 121 = 12² |
Voir
problème de Brocard en 4 |
|
Puissance
|
n² = {5k – 1, 5k, 5k +
1} |
|
|
5 = 1² + 2² |
|
|
5 = 2² + 1 |
|
|
5 = 3² – 2² 5 = 25 –
33 |
|
|
3² – 2² = 5 34
– 24 = 65 3n
– 2n = ….5 |
|
|
5 = 4.14 + 14 |
|
|
|
|
![]()

Différences
entre puissances de 5
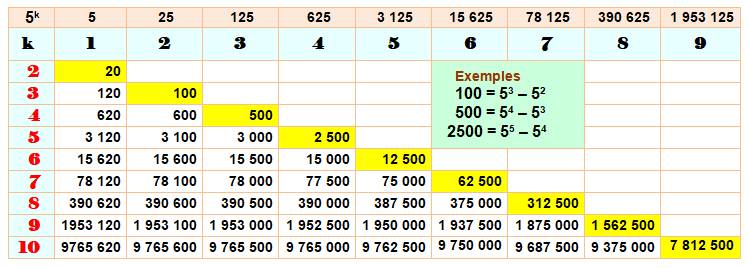
Voir Puissance
/ Racine
/ Nombre 100 / Nombre 500
|
1² + 24 = 5²
et 5² + 24 = 7² |
|
||
|
5² = 25 |
|
||
|
|
|
||
|
5² = 13² – 12² = 13 +
12 |
|
||
|
52 – 1 = 24 54 – 1 = 624 56 – 1 = 15624 58 – 1 = 390624 … |
Sinon
(impair): divisible par 4. |
||
|
52 – 33 = –2 = 27 – 25 |
Différence
entre un cube et un carré. |
||
|
53 = 125 54
= 625 83 = 512 44 = 256 |
|
||
|
53 = 125 et 1+2+ 5 = 8 = 23 |
|
||
|
|
|
||
|
53 = 2² + 11² =
5² + 10² |
|
||
|
54 = 625 = 164 + 461 = 263 + 362 |
Voir:
10 340 + 4 301 = 14 641 = 114. |
||
|
54 = 7² + 24² = 625 |
|
||
|
54 = 24 + 24 + 34 + 44 + 44
= 16 + 16 + 81 + 256 + 256 = 625 |
|
||
|
…a5 = …a Ex: 115
= 161051 |
|
||
|
5k = … 5 |
|
||
|
…u5 = … u |
Devinette
|
||
|
25 = 32 et 3 + 2 = 5 |
|
||
|
25 + 5 = 37 |
|||
|
275 +
845 + 1105 + 1335 = 1445 |
Trouvé
en 1967 par Léon Lander, Thomas Parkin et John Lewis Selfridge. |
||
|
|
|
||
|
|
Seuls tels nombres avec p = (3, 5, 17 et
157). |
||
Calculs
de folie …

Voir Fractions
illicites
Jeux
et curiosités
|
5 = (11 x 11 – 11) / (11 + 11) |
|
|
|
|
|
|
|
|
(5, 07432 61995 23190 4416…) 4 = 28² – 11² = 663 6631/4
= 5,0743261995 2319044158 1607842208 5245815311 7475502912… |
|
|
|
|
||
Suite sur
les décimales >>>
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
|
|
2, [1, 0, 1] 3,
[1, 2] |
4,
[1, 1] 5,
[1, 0] |
4,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()