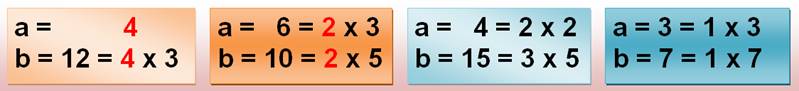|
|||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ Sujet incontournable, exercice imposé. Comme les gammes pour apprendre le piano. Cette première page introduit simplement les notions abordées dans les
pages suivantes:
Pas difficile, et même très intuitif. Mais mérite d'y passer un petit
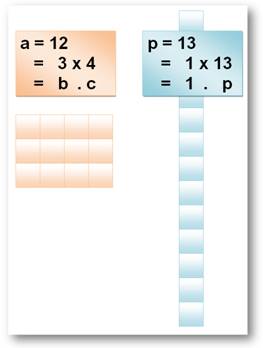
peu de temps pour bien s'imprégner. C'est fondamental pour la suite. Notations: on ne sait jamais où les chercher ! Personnellement, je conserve le point pour
signifier multiplication: a . b Beaucoup d'ouvrages l'omettent: ab |
Tous les nombres n'ont pas la même façon de
se comporter!
|
|
Voir Pensées & humour
/ Introduction aux nombres
géométriques
|
|
|||
|
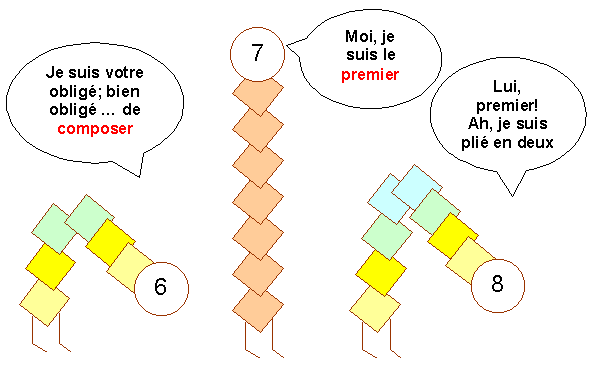
Premier cas: nombre COMPOSÉ >>> Le nombre
"se laisse" faire. |
|
Second cas: nombre PREMIER >>> Il refuse de
" se plier" à notre volonté. |
|
|
|
|
||
|
|
||||
|
L'un divise l'autre |
Tous deux "un peu" divisibles |
Premiers entre eux |
Tous deux premiers |
|
|
|
||||
|
Un nombre au moins est composé |
Deux nombres premiers |
|||
|
|
|
ils sont
différents.
|
|
|
|
Divisibles |
Non divisibles, mais un peu divisibles |
Non divisibles >>> |
||
|
Premiers entre eux |
A fortiori, premiers entre eux |
|||
Récapitulatif des cas possibles selon la
nature des deux nombres
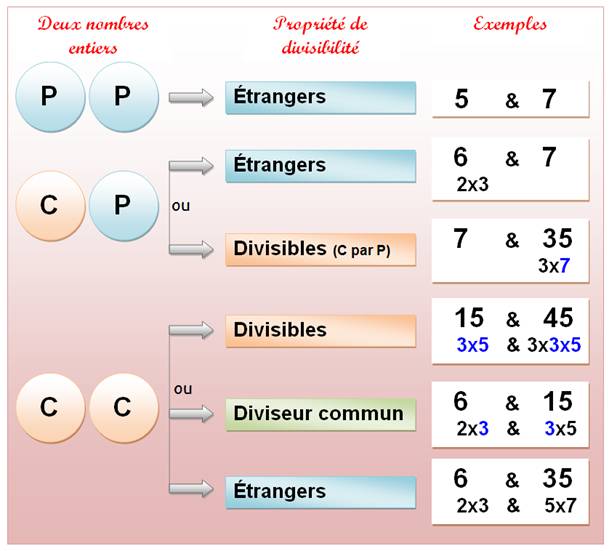
Pour ceux qui aiment les tableaux logiques
(l'aire n'est pas
représentative de la quantité de cas; idée topologique seulement)
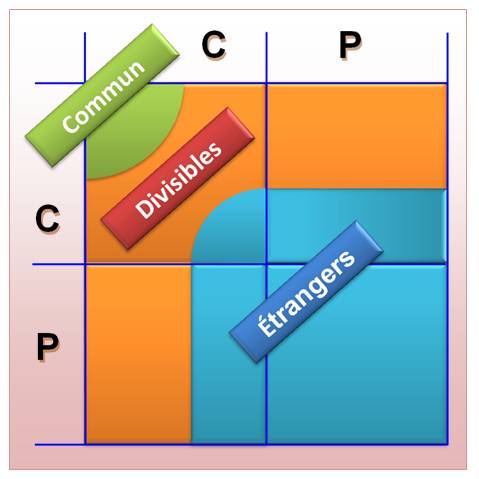
|
|
||||||||||||||||||||||
|
|
a, b, q et r sont des
nombres entiers. b est premier ou composé. a est premier ou composé. Exemples
|
|||||||||||||||||||||
|
|
Diviseurs de
140
84
2 x 2 x 7 = 28 Alors 28 divise
aussi bien 140 que 48.
2 x 2 x 3 x 5 x 7 = 420 Alors 420 est
divisible par 140 et par 84. |
|||||||||||||||||||||
|
|
||
|
|
a, b et d sont des
nombres entiers a et d sont des diviseurs de b. b est un multiple de a. Diviseurs de
4 12 60 |
|
Bilan
|
Nous venons d'introduire les notions
suivantes:
|
![]()
|
Retour |
|
|
Suite |
|
|
Autour |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/DivAppro.htm
|
![]()