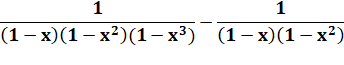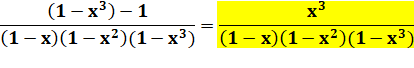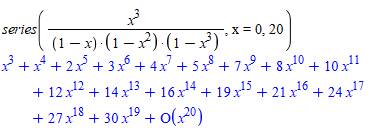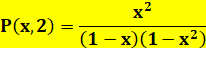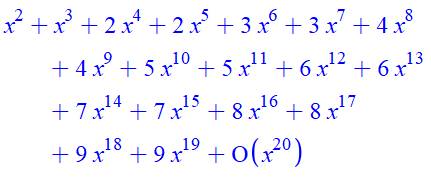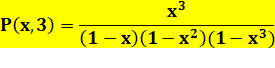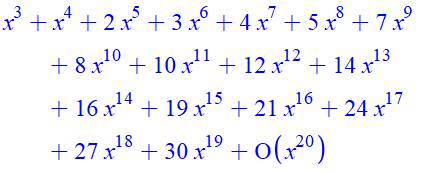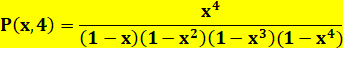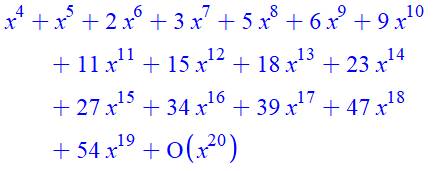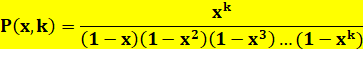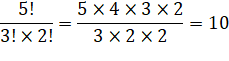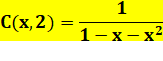|
|||||||||||||||||||||||||||||||||
![]()
|
PARTITIONS des nombres Quantité et polynômes générateurs Revue des polynômes dont les coefficients indiquent la quantité de
partitions d'un nombre dans certaines conditions. Surprise de rerouver la suite de
Fibonacci ou ses cousines les k-bonacci. On notera bien la distinction entre:
|
Anglais:
partition, composition, sommand or addend
|
|
|||
|
But Voyons la
partition du nombre 7. On cherche
à connaitre cette quantité pour tous les nombres. |
Partition de 7 [1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 2], [1, 1, 1, 2, 2], [1, 1, 1, 1, 3], [1, 2, 2, 2], [1, 1, 2, 3], [1,
1, 1, 4], [2, 2, 3], [1, 3, 3], [1, 2, 4], [1, 1, 5], [3, 4], [2, 5], [1, 6], [7] |
||
|
Programme
|
Commentaires Le programme est en deux
parties:
La procédure commence
en faisant appel au logiciel spécialisé en combinatoire et en calcul de
partitions (combinat). Le compteur de partitions kt est initialisé à 0. On place la liste des
partitions dans PN et on calcule la quantité
de terme (qPN). La boucle sert à reconnaitre
les partitions à k termes. Chaque partition PN[i] est examinée. La quantité de nombres qI est comparée à k
pour faire progresser le compteur kt. La procédure retourne ce
nombre kt, quantité de fois où le nombre de
termes de la partition est égal à k. Le programme
principal calcule la suite la quantité de partitions (QP) du nombre n en k
sommants pour tous les nombres de n égal 1 à 50. Résultat Liste pour les nombres de 1
à 50 des quantités de partitions de trois termes. Pour le nombre 7, on
retrouve bien kt = 4 en septième position. Voir Programmation – Index Programmation de la
quantité de partitions avec formule récursive |
||
|
Polynôme
générateur Ce
polynôme engendre la suite des quantités de partions de trois termes |
|
||
|
En le développant
en série |
|
||
|
|
||
|
Pour 2
sommants P(7, 2) = 3 |
Liste 0, 1, 1, 2, 2, 3, 3,
4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10 … Polynôme
générateur
|
|
|
Pour 3
sommants P(7, 3) = 4 |
Liste 0, 0, 1, 1, 2, 3, 4,
5, 7, 8, 10, 12, 14, 16, 19, 21, 24, 27, 30, 33… Polynôme
générateur
|
|
|
Pour 4
sommants P(7, 4) = 3 |
Liste 0, 0, 0, 1, 1, 2, 3,
5, 6, 9, 11, 15, 18, 23, 27, 34, 39, 47, 54, 64 … Polynôme
générateur
|
|
|
Pour k
sommants |
Polynôme
générateur
|
|
|
|
||
|
But Voyons la
partition du nombre 7. C(7, 2) = 21 Pour [1,
1, 1, 2, 2], il y a 5! permutations, mais 3! sont identiques avec les 1 et 2!
avec les 2. Si bien que la quantité de permutations effective est:
Ces calculs sont traités en détail sur les pages Escalier 2
et Escalier
3 |
Partition de 7 [1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 2], [1, 1, 1, 2, 2], [1, 1, 1, 1, 3], [1, 2, 2, 2], [1, 1, 2,
3], [1, 1, 1, 4], [2, 2, 3], [1, 3, 3], [1, 2, 4], [1, 1, 5], [3, 4], [2, 5], [1, 6], [7] Composition de
7 par 1 et 2 [1, 1, 1, 1, 1, 1, 1] => 1
permutation [1, 1, 1, 1, 1, 2] => 6
permutations [1, 1, 1, 2, 2] => 10 permutations [1, 2, 2, 2] => 4 permutations Total: 21 permutations
= quantité de compositions |
|
|
Polynômes
générateurs Ces
polynômes donnent à la fois les quantités de compositions et les nombres
de Fibonacci généralisés comme les tribonacci
et tous les k-bonacci. Ils sont étudiés et programmés en: Polynômes
générateurs des nombres k-bonacci. |
Polynômes
générateurs
|
|
|
C(3,3) = [ [1 + 1 + 1], [1 + 2], [2
+ 1], [3] ] Transformation en somme de produit E = (1 x 1 x 1) + (1 x 2) + (2 x 1)
+ (3) = 1 + 2 + 2 + 3 = 8 Or 8 est le sixième (2x3) nombre de Fibonacci (1, 1, 2, 3, 5, 8 …) C(4,4) = [ [1, 1, 1, 1], [1, 1, 2],
[2, 2], [1, 3], [4] ] Transformation en somme de produit en tenant compte des
permutations E = (1 x 1 x 1 x 1) + 3(1 x 1 x 2) + (2 x 2) + 2(1, 3) + 4 = 21 Or 21 est le huitième (2x4) nombre de Fibonacci (… 5, 8, 13, 21 …) On
note la relation: C(n, n) = F2n La quantité de compositions complètes
de n est égale au nombre de Fibonacci de rang double. |
Source: Relationship
between Ordered Compositions and Fibonacci Numbers – Soumendra Bera - 2015
|
|
||
|
Partitions of a positive integer n
including permutations of the parts or summands
are called compositions of n. There exists a definite order of the
compositions of n, which has close connection with the Fibonacci sequence. The partition function gives the number of
ways of writing the integer n as a sum of positive integers, where the order
of addends is not considered
significant. |
For example, eight compositions of 4 are: [4], [3 + 1], [1 + 3], [2 + 2], [2 + 1 + 1], [1 + 2 + 1], [1 + 1 + 2], [1 + 1 + 1 + 1]. |
|
![]()
|
Retour |
|
|
Suite |
|
|
En savoir plus |
|
|
Références |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/PartitiG.htm |
![]()