NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 26/01/2018

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique       Brèves de Maths    

            

Théorie des Nombres

 

Débutants

Nombres

COURS

 

Glossaire

Nombres

 

 

INDEX

 

Sommaire

 

Partitions

Accueil

Nombres

Partition (1/2)

Partition (2/2)

Partition PG

Partition en couleurs

Terminale

 

Sommaire de cette page

>>> Orientation

>>> Approche

>>> Au début: de 1 à 5

>>> Construction pour 6

Sur page suivante

>>> Application au 7

>>> Table de à 15

>>> Propriétés

 

 

 

 

 

PARTITION des NOMBRES

 

Comportement des nombres face aux opérations.

 

Addition

 PARTITION

 

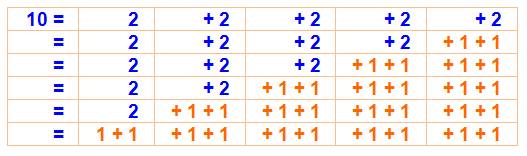
Exemple: 10 = 1 + 2 + 3 + 4

 

>>>

 

Multiplication

 DÉCOMPOSITION en FACTEURS

 

Exemple: 10 = 1 x 2 x 5

 

>>>

 

 

 

 

Orientation

 

Partition

 

Décomposition d'un nombre en somme de nombres appelés sommants.

 

Analogies

Pesée des nombres.

Voir Pesées de Leibniz et de Bachet

 

 

Combien?

Combien de manières existe-t-il de décomposer un nombre en somme de nombres ?

Quelle est la quantité de partitions d'un nombre?

 

Calcul

Le dénombrement des partitions d'un nombre n'est pas évident. Il n'y a pas de formule simple. Vous trouverez sur cette page la manière de les compter.

 

 

Je souhaite connaître:

 

 

Anglais: Partition of  the integers

The number p(n) of partitions of an integer n into summands

 

 

Approche

– Comment peser 10 kg avec des poids de valeur 2 et 1 kg

 

 

*    Nous comptons six possibilités, appelées PARTITIONS dont 5 avec au moins un poids de 2 kg et 1 avec des poids de 1 kg seulement. Nous noterons:

*    P102 = 5

*    P101 = 1

*    Bien sûr, nous aurions pu utiliser des poids de 3, 4 … kg. Patience!

 

 

 

 

Au début: de 1 à 5

 

Partition des premiers nombres

 

 

N = 1

2

3

4

5

p = 1

1

1 + 1

1 + 1 + 1

1 + 1 + 1 + 1

1 + 1 + 1 + 1 + 1

2

 

2

2 + 1

2 + 1 + 1

2 + 2

2 + 1 + 1 + 1

2 + 2 + 1

3

 

 

3

3 + 1

3 + 1 + 1

3 + 2

4

 

 

 

4

4 + 1

5

 

 

 

 

5

 

*    Chaque colonne indique les partitions possibles du nombre N indiqué en tête de colonne

*    Chaque ligne représente toutes les "pesées" comprenant au moins une fois le "poids" p indiqué" en tête de ligne

 

Notons la quantité de partitions

 

 

1

2

3

4

5

p = 1

1

1

1

1

1

2

 

1

1

2

2

3

 

 

1

1

2

4

 

 

 

1

1

5

 

 

 

 

1

Quantité de partitions

1

2

3

5

7

 

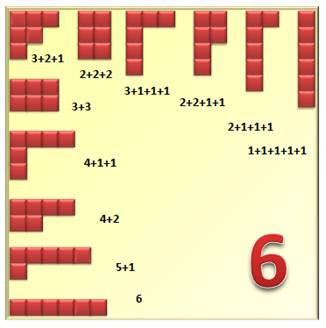
Lecture: Le nombre 5 peut être décomposé en 7 sommes ou partitions ou 6 partitions propres, en retirant la partition de 5 par lui-même.

 

 

 

 

CONSTRUCTION pour 6

 

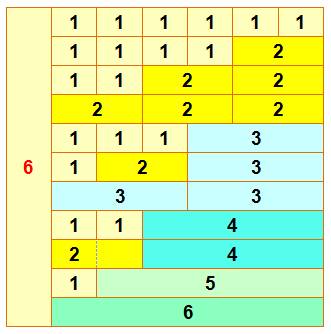
Partition du 6 avec que des 1

 

 

6

Commentaires

Quantité

p = 1

1 + 1 + 1 + 1 + 1 + 1

Une seule possibilité.

Comme pour son voisin le 5.

 

1

 

Notons ce résultat de la façon suivante, en profitant du tableau que nous avons élaboré pour 1 à 5.

 

1

2

3

4

5

6

1

1

1

1

1

1

1

2

 

1

1

2

2

 

3

 

 

1

1

2

 

4

 

 

 

1

1

 

5

 

 

 

 

1

 

 

Voyons la partition de niveau 2

 

 

6

Commentaires

Quantité

2

2 + quatre

À ce niveau de "pesée" nous devons mettre au moins un 2

Il nous reste 6 – 2 = 4 à peser avec des 2 ou des 1

Or "4" pesé avec des 2 donne 2 possibilités

Et "4" pesé avec des 1 n'en donne qu'une

 

2

+1

= 3

 

Notons ce résultat de la façon suivante:

 

1

2

3

4

5

6

1

1

1

1

1

1

1

2

 

1

1

2

2

3

3

 

 

1

1

2

 

4

 

 

 

1

1

 

5

 

 

 

 

1

 

Lecture: en ligne du 2, je pose 3 en colonne du 6, car j'ai 1 + 2 = 3 en colonne du 4.

 

Partition de niveau 3

 

6

Commentaires

Quantité

3

3 + trois

À ce niveau de "pesée" nous devons mettre au moins un 3

Il nous reste 6 – 3 = 3 à peser avec des 3, des 2 ou des 1

Or "3" pesé avec des 3 donne 1 possibilité

     "3" pesé avec des 2 donne 1 possibilité

Et "3" pesé avec des 1 n'en donne qu'une

 

1

+1

+1

= 3

 

Notons ce résultat de la façon suivante:

 

1

2

3

4

5

6

1

1

1

1

1

1

1

2

 

1

1

2

2

3

3

 

 

1

1

2

3

4

 

 

 

1

1

 

5

 

 

 

 

1

 

 

Partition de niveau 4

 

6

Commentaires

Quantité

4

4 + deux

À ce niveau de "pesée" nous devons mettre au moins un 4

Il nous reste 6 – 4 = 2 à peser avec des 4, des 3, des 2 ou des 1

Or "2" pesé avec des 4 donne 0 possibilité

     "2" pesé avec des 3 donne 0 possibilité

     "2" pesé avec des 2 donne 1 possibilité

Et  "2" pesé avec des 1 donne 1 possibilité

 

 

0

+0

+1

+1

= 2

 

Notons ce résultat de la façon suivante:

 

1

2

3

4

5

6

1

1

1

1

1

1

1

2

 

1

1

2

2

3

3

 

 

1

1

2

3

4

 

 

 

1

1

2

5

 

 

 

 

1

 

 

Partition de niveau 5

 

6

Commentaires

Quantité

5

5 + un

À ce niveau de "pesée" nous devons mettre au moins un 5

Il nous reste 6 – 5 = 1

Une seule possibilité

 

 

= 1

 

Notons ce résultat de la façon suivante

 

1

2

3

4

5

6

1

1

1

1

1

1

1

2

 

1

1

2

2

3

3

 

 

1

1

2

3

4

 

 

 

1

1

2

5

 

 

 

 

1

1

 

Partition de niveau 6

 

6

Commentaires

Quantité

2

6 + 0

Une seule possibilité

= 1

 

Notons ce résultat de la façon suivante:

 

1

2

3

4

5

6

1

1

1

1

1

1

1

2

 

1

1

2

2

3

3

 

 

1

1

2

3

4

 

 

 

1

1

2

5

 

 

 

 

1

1

6

 

 

 

 

 

1

 

Quantité de partitions

 

1

2

3

4

5

6

1

1

1

1

1

1

1

2

 

1

1

2

2

3

3

 

 

1

1

2

3

4

 

 

 

1

1

2

5

 

 

 

 

1

1

6

 

 

 

 

 

1

Quantité de partitions

1

2

3

3

1

 

 

Somme 10

Somme 10

+1 Pour le 6 par lui-même

 

 

 

Quantité de partitions du nombre 6 : 10 + 1

 

 

Voir Diagramme de Ferrers

 

 

 

Conclusions

La somme des nombres dans le triangle coloré est égale à la quantité de partitions propres du 6 (hors le 6 par le 6).

 

Il est possible de calculer les valeurs des partitions du 6 en fonction des valeurs déjà connues pour les partitions des nombres inférieurs.

 

 

 

 

 

 

 

 

Retour

Suite

*         Théorème fondamental de l'arithmétique

*         Partition (suite)

*         Partitions et jeu de dés – Formule et calculs

*         Rectangles magiques à répétitions

*         Polygones à périmètre magique

En savoir plus

*         Addition – Glossaire  

*         Conjecture de Goldbach

*         Escalier et partitions

*         Nombre d'Ulam

*         Nombres quatrops

*         Nombres (représentation)

*        Partition en couleurs

*         Partition des nombres de 1 à 10

*         Partitions – Développements 

*         Partitions – Fonctions génératrices

*         Somme des nombres impairs

Références

*         DicoMot

*         DicoNombre

*         Glossaire mathématique

Voir

*         Calcul – Index

*           Conjecture de Goldbach

*         Jeux et puzzles – Index

*         Nombres modulo

*         Nombres par leur petit nom

*         Systématique – Index

*           Théorie des Nombres – Index

Cette page

http://villemin.gerard.free.fr/Referenc/Prof/APROF/Partitio.htm