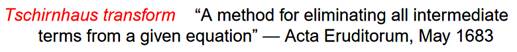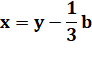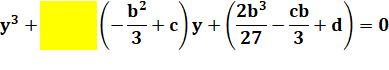|
Édition du: 08/07/2023 |
|
INDEX |
ÉQUATIONS |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Réduction des équations Nombres d'Hamilton Comment diminuer
le nombre de termes dans une équation de degré n ? Combien de termes ? |
||
|
|
Sommaire de cette page >>> Réduction >>> Principe de la transformation et exemples >>> Polynômes réduits >>> Nombres d'Hamilton |
Débutants Glossaire |
Anglais: Hamilton number or
resolvent degree
|
Approche |
Hamilton
(1805-1865), dans son rapport de 1836 à l'Association britannique, indique
qu'il est possible d'arriver à trouver des solutions plus simples à un
problème de résolution d'équations. L'origine de la méthode remonte à Tschirnhaus
(1651-1708). En 1683, il annonce qu'il a trouvé une méthode algébrique pour déterminer
les racines d'un polynôme de degré n. Même si sa déclaration s'est avérée
fausse, sa méthode de transformation a été adoptée.
|
|
|
Transformation |
La transformation consiste à remplacer un
polynôme de degré k par un autre comportant moins de termes. Cad: en éliminant
des termes de puissances inférieures à k. Combien peut-on en éliminer ? Ce
seront les nombres d'Hamilton. La transformation n'est pas simple et parfois
impossible en solutions avec radicaux.
De plus, elle nécessite la résolution d'équations de degré de 1 à k. En 1786, Bring a montré que lorsque k > 4 on
peut trouver les solutions en résolvant des équations de degré 1, 2 et 3 (pas
plus). En 1834, Jerrand annonce confimer ces résultats:
il est possible de retirer trois termes à une quintique en utilisant la
transformation de Tschirnhaus. En revanche, il s'obstine à vouloir résoudre
de telles équations du cinquième degré alors qu'il savait qu'Abel avait
démontré l'insolvabilité (1824). En 1837, Hamilton montre que ces résultats sont erronés! Il montre qu'il est possible d'éliminer
quatre termes pour le degré 11 et cinq termes pour le degré 47. Depuis, les travaux sur ce sujet se poursuivent.
But: élaborer des méthodes pour trouver pratiquement la réduite d'un
polynôme. Les logiciels de calcul Maple, Mathematica offrent des
outils pour résoudre ces équations (resultant function) |
|
Principe de la transformation et exemples
|
Principe Prenons une
cubique |
|
|
Un
changement de variable |
|
|
Nouvelle
cubique |
|
|
Élimination |
On peur
éliminer y² ou y en posant que le coefficient est égal à 0. Il s'agit
alors de résoudre des équations de degré 1 et de degré 2 et non de degré 3. |
|
Transformation |
Tschirnhaus généralise et pose:
Alors m
termes intermédiaires peuvent être éliminés simultanément sous m conditions. |
|
Exemple: degré 3 cubique |
|
|
Transformation
de Descartes |
|
|
En
remplaçant: Un terme en moins ! |
|
|
Exemple: degré5 Quintique |
|
|
Changement
de variable |
|
|
Nouvelle
quintique |
|
|
Avec |
|
|
Avec c1
= c2 = 0 |
|
|
En
remplaçant: Deux termes en moins ! |
|
D'après A New
Way To Derive The Bring-Jerrard Quintic In Radicals – Titus Piezas III
|
Deuxième degré H2 = 1 |
On sait généralement qu'en présence d'une
équation quadratique, ou de degré supérieur, il est possible d'effectuer une transformation éliminant le deuxième terme. |
|
|
Troisième degré H3 = 2 |
Tschirnhaus a montré qu'une équation cubique, et
toutes les équations de degrés supérieurs, pouvaient être privées de leurs
deuxième et troisième termes en résolvant des équations linéaires et
quadratiques. |
|
|
Cinquième degré H5 = 3 |
En 1786, Bring, de l'Université de Lund, montra que
toute équation du 5e degré, ou de tout degré supérieur, pouvait
être privée de ses trois premiers termes en résolvant certaines équations quadratiques,
cubiques et linéaires. |
|
|
La suite ? |
Quelle est la suite de H2, H3,
H5 ? Les indices (2, 3, 5) témoignent du degré de l'équation que
l'on peut réduire. Il faut aller au 11e degré pour pouvoir retirer
quatre termes. Quel est le degré le
plus bas qu'une équation puisse avoir pour qu'elle puisse admettre
d'être privée de cinq termes consécutifs à
l'aide d'équations des 1er, 2e, 3e et 4e
degrés. Ou plus généralement de k termes consécutifs à
l'aide d'équations de degré inférieur à k. |
|
|
Définition |
Le nombre d'Hamilton est le degré minimal d'une
équation dont on peut retirer n termes successifs après le premier par une
suite de transformations comparables à celle de Tschirnhaus sans exiger la
solution d'une équation de degré supérieur à n. Hamilton a calculé les six premiers termes de
cette séquence. C'est la raison pour laquelle Sylvester et Hammond les ont
nommés "nombres de Hamilton".
|
|
|
Nombres d'Hamilton |
2, 3, 5, 11, 47, 923,
409619, 83763206255, 3508125906290858798171,
6153473687096578758448522809275077520433167, … |
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |