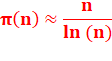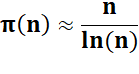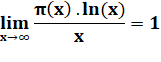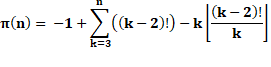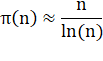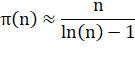|
|||||||||||||||||||||||||||||||||||||||||||||
NP: Nombres premiers
![]()
|
Théorème des NOMBRES PREMIERS La proportion de nombres premiers Autrement dit: Le pourcentage de
nombres premiers existants est nul. |
Voir Pourcentage
|
des
nombres premiers |
|
||||
|
Formes
équivalentes
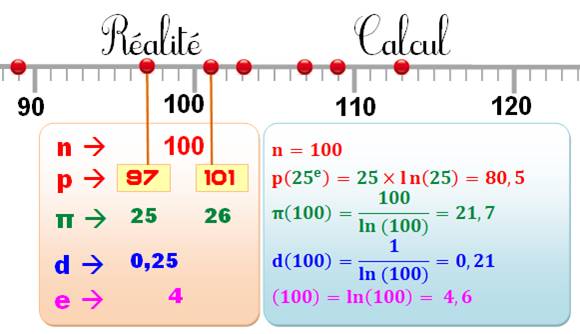
Notez bien la mention "environ".
Valeurs d'autant plus proches que n est grand. Exemple
de calcul pour n = 100 et k = 25
|
|||||
Anglais: Prime Number Theorem
Voir Écarts entre
nombres premiers / Barre magique
des nombres premiers
Merci à Jean-Michel
Moinade pour ses remarques
|
|
|||||
|
Théorème
Autre
formulation
Encore
plus proche
|
|
||||
|
|
||||||||||||
|
Théorème
|
Tableau
en puissances de dix
Voir Historique |
|||||||||||
|
Théorème
|
Exemple
|
|||||||||||
|
|
|||||
|
Théorème
|
Le
millionième premier est: n = 1 000 000
Notez que n est le rang du nombre premier. |
||||
Suite et développements
en Encadrement des nombres premiers
|
|
|
|
|
|
ln(x) ou Log (x) |
|
|
|
log(x) |
|
|
|
ln(x) = 2,3026… x log(x) |
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()