|
Édition du: 26/02/2023 |
|
INDEX |
PARTITIONS principales |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Partitions non-croisées Nombres des chemins polygonaux Partitions
particulières d'un ensemble qui représentées graphiquement couvrent des
surfaces distinctes. |
||
|
|
Sommaire de cette page >>> Le |
Débutants Glossaire |
|
Approche |
||
|
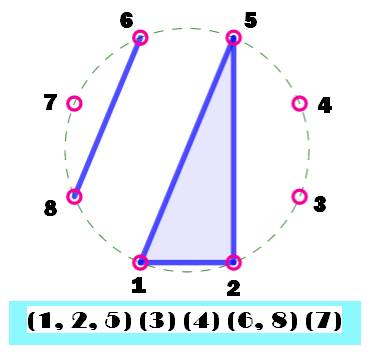
Interprétation figurée Soit un ensemble de huit éléments représentés par
huit points sur un cercle. Une façon de représenter leurs partitions
consiste à associer des points entre eux. La partition est non croisée si les surfaces,
lignes et points créés ne se rencontrent pas. Interprétation arithmétique La formulation arithmétique est moins évidente. Soit une partition de {1, 2, 3, …, n} en k bocs. Une partition est non-croisées s'il n'existe pas
quatre nombres a < b < c < d
tels que a et c sont dans un bloc et b et d dans un autre. |
|
|
|
Partition de
5 éléments |
|||||||
|
Les 42 partitions non-croisées de
cinq éléments On montre la configuration de base. En général
dix autres s'en déduisent par rotations et symétries. En dessous, la partition exprimée en nombres.
|
|||||||
|
10
fois |
10 |
10 |
10 |
10 |
1 |
1 |
|
|
(1,2)(3)(4)(5) |
(1,2,4)(3)(5) |
(1,5)(2,3)(4) |
(1,2)(3,4,5) |
(1,2,3,5)(4) |
(1,2,3,4,5) |
( ⌀ ) |
|
|
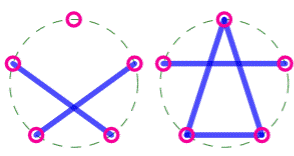
Les 10 partitions croisées de cinq
éléments Il existe 10 = (2 × 5) autres partitions de cinq éléments qui sont croisées.
|
|||||||
|
Le |
||
|
Dénombrement |
La
quantité de partitions d'un ensemble de n éléments est égale au nième nombre de
Catalan. Liste: 1, 1, 2, 5, 14, 42, 132, 429, 1430,
4862, … >>> Exemple: C5 = 42 pour 42 partitions
non-croises de cinq éléments. |
|
|
|
||
|
An On |
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/PttCrois.htm |