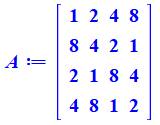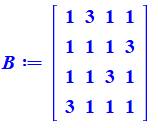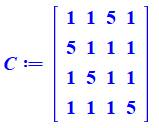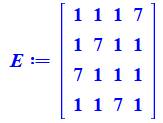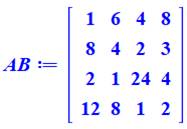|
|||||||||||||||||||||||||||||
![]()
|
Remplir la grille avec
les nombres de 1 à 8, chacun étant
éloigné de son voisin
immédiat. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Choix
des nombres
Disposition
Ordre 3
Résultat
9078 + 9240 + 9360
= 9256 + 9072 + 9350 = 27678
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||
|
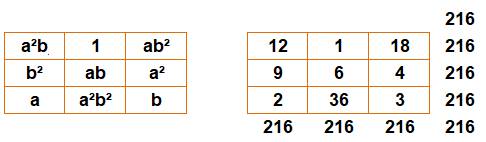
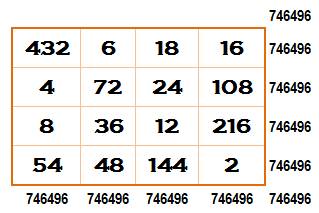
Multiplicatif
Carré
multiplicatif d'ordre 3 – Générique et exemple avec a = 2 et b = 3
Ce
carré a sans doute été trouvé en 1893 par G. Pfeffermann. Il est cité par Harry A. Sayles en 1913. Sa
constante magique est 216, nombre qui est le plus petit possible, démontré en
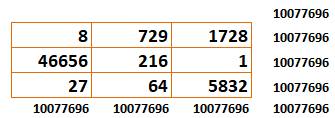
1983. Comme
tout carré magique multiplicatif, celui-ci reste magique lorsque chacun des
nombres est élevé à la puissance k.
Il
est impossible de construire un carré magique multiplicatif avec des nombres
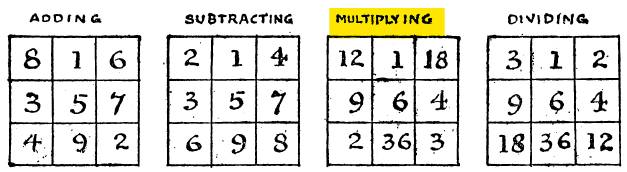
entiers consécutifs. Un
carré magique additif est transformé en carré magique multiplicatif en
utilisant ses nombres comme les exposants d'un nombre quelconque.
Henry
Dudeney publie ces carrés en 1917 dans son livre Amusements in Mathematics
|
||||||||||
|
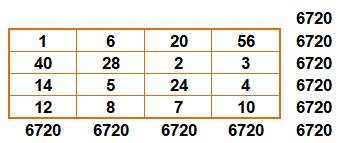
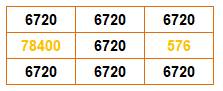
Exemples d'ordre 4 Celui-ci est aussi bien
complet (auteur: King):
Un autre carré magique
multiplicatif.
Ce carré est produit
par les multiplications
d'Hadamard successives de ces quatre matrices:
|
Voir Carré magique multiplicatif 7x7
|
Additif
et multiplicatif (auteur Dénes and Keedwell )
L'astuce
est de profiter du caractère additif des exposants lors d'une multiplication
de puissances. Les exposants forment un
carré magique additif; les nombres en puissance
de 2 forment un carré magique multiplicatif. La constante magique est
égale à 212 = 4096. Le
carré reste doublement magique pour tout autre nombre que 2, mais supérieur à
2. |
|
|
|||||||||||
|
|
|||||||||||
|
Ordre
3 Formé avec
les entiers les plus petits
|
|
||||||||||
|
Forme
générique
|
|
||||||||||
Voir Suite
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Nombres têtus
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
Somme 60 |
Somme 204 |
|||||||||||||||||||||||||||||||||
|
Carré magique à MOTIFS |
|
|||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
Esthétique
Somme 264 |
Nombres
pairs de 2 à 32
Somme 68 |
|||||||||||||||||||||||||||||||||
|
Remplir
la grille avec les nombres de
1 à 8, chacun étant éloigné de
son voisin immédiat. |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()
Renvois
de liens
CARRÉS ALPHA MAGIQUES >>>
SOMMES ET COUPLES >>>
JEUX DE CARRÉ MAGIQUE >>>
DOMINOS MAGIQUES >>>