|
|||||||||||||||||||||||||||||
![]()
|
CARRÉS MAGIQUES avec des nombres au carré Faisabilité
et exemples de carrés magiques formés avec des nombres au carré. Les carrés sont distincts, non nécessairement
consécutifs, évidemment. Alors que
de tels carrés existent pour l'ordre 4 et plus, on ne connait pas encore de
carré d'ordre 3. On cherche toujours la démonstration pour prouver leur
non-existence. |
Anglais: Magc square of squares
|
avec le maximum de carrés |
|
|
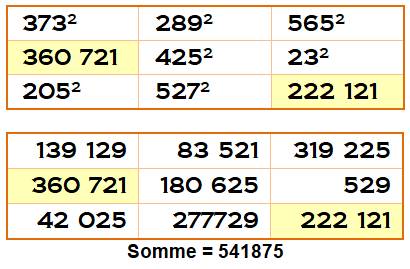
Record depuis 1997 Seul exemple avec le maximum de carrés pour un carré 3x3. Il y a 7 carrés sur 9. Par de carré magique connu avec 8 ou 9 carrés .
Carré trouvé indépendamment par Andrew Bremmer et Lee Swallows en
1997. Carrés magiques avec quelques nombres au carré
|
|
|
Carrés
semi-magiques d’ordre 3 avec des nombres au carré |
|
|
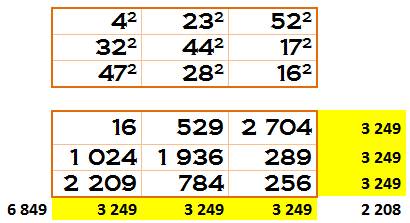
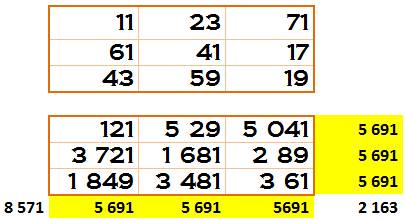
Exemple à 4 sommes magiques dont les diagonales
Exemple à 6 sommes magiques sans les diagonales
3 249 = 57² Ce carré est un carré semi-magique
de nombres carrés et en anglais: orthomagic square of squares (OMSOS). Carré semi-magique avec nombres premiers au carré
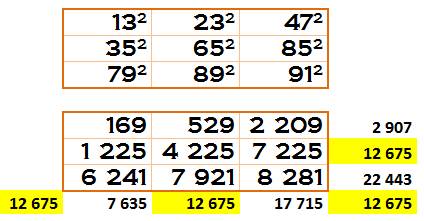
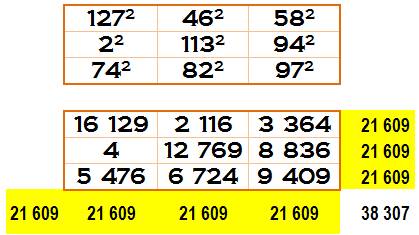
Exemple à 7 sommes magiques; une seule diagonale
manque
21 609 = 147² Ce carré, avec sept sommes magiques, est dû à Lee Sallows (The
Mathematical Intelligence) et indépendamment à Michael Cette exploration n'est pas compliquée à programmer. Il suffit de
boucler sur quatre variables seulement. Par contre, le temps d'exploration
peut être long. |
|
|
les carrés
de carrés d'ordre 3 |
|
|
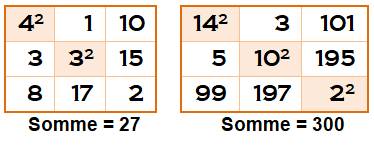
Ces trois configurations
sont donc possibles, mais impossible de réaliser le carré magique complet
avec des nombres au carré. On démontre effectivement que
c'est impossible dans certains cas, mais la preuve n'est pas exhaustive.
Comme pour le théorème
de Fermat-Wiles, il semble qu'il faille avoir recours à une transposition
sur d'autres problèmes équivalents et à des outils très avancés des
mathématiques En 1984, Martin Labar pose la
question: est-ce qu'un carré magique 3x3 peut être construit avec neuf
nombres carrés distincts? Les recherches sont lancées. Il s'agit de trouver
un exemple, ou alors la démonstration
prouvant la non-existence. En 1996, Martin Gardner repose la même question en affirmant: s'il
existe, ses nombres sont énormes, peut-être hors de portée des ordinateurs actuels les plus
puissants. John Robertson a montré que les problèmes mathématiques suivants sont
liés:
Dans son livre Unsolved Problems in Number theory (2004), Richard Guy
fait le point des recherches.
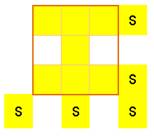
Duncan Buell a montré qu'il n'y a aucune solution pour cette forme en
sablier jusqu'à 2,5 1025 |
|
Voir Carrés magiques avec premiers / Nombres premiers / Carrés bi-magiques
Un petit calcul pour de grandes conséquences
|
Dans un carré
magique 3x3, la somme des sommets
opposés est égale à deux fois l'élément central. Ici, en l'occurrence avec
des carrés: x² + y² = 2z². Cette équation diophantienne a bien des solutions:
1² + 7² = 2 x 5². Tout va bien jusque là pour le carré 3x3 de carrés. Par contre, à une
puissance p supérieure à 2, il n'y a pas de solution (conséquence du théorème de
Fermat-Wiles). Ce qui veut dire que Il n'existe pas de carré magique 3x3 avec des cubes, des puissances 4 ou au-delà. |
![]()
|
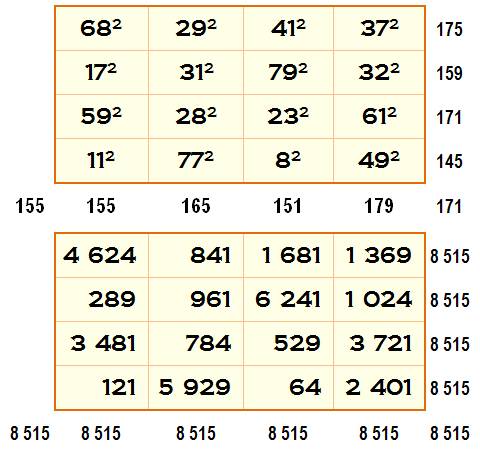
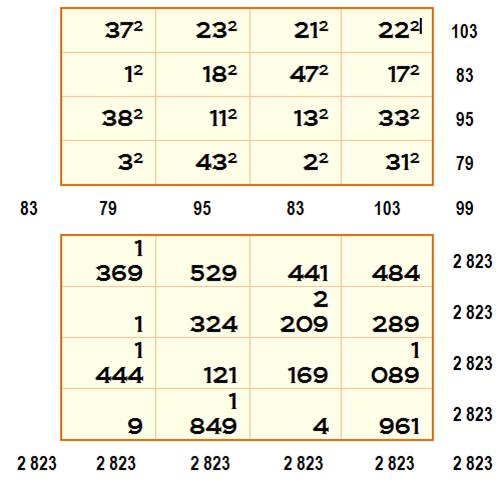
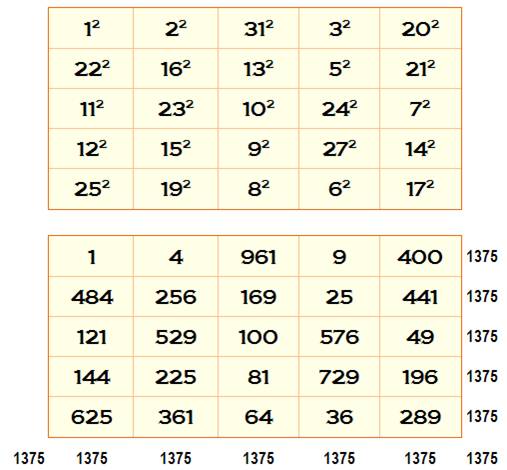
Carrés
semi-magiques d’ordre 4 avec des nombres au carré |
|
|
Carré magique de Christian Boyer (2005)
Les nombres utilisés 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 |
|
![]()
|
Suite |
|
|
Voir |
|
|
Voir toutes les autres références sur les carrés magiques |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaCMag/CarCarre.htm
|
![]()