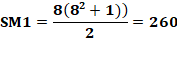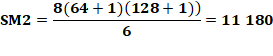NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/05/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Bases et amusements				Glossaire Carrés magiques
INDEX Carrés magiques Ordres Constructions Magie Jeux de grilles Jeux et énigmes	Latin	Gréco-latin	Avec 0 à 9		Vers Magiques
	Multi-magiques	Jeux (à trous)	Décimal		Sudoku
		Premier	Pannum. premier		Inverse premiers
		Sommaire de cette page >>> Carré ou bi-magique ? >>> Bi-magique ? >>> BI – Ordre 8		>>> BI – Ordre 9 >>> BI – Ordre 6 (presque) >>> TRI – Ordre 12 >>> Propriétés et historique >>> Anglais

Carrés multi-magiques

Le carré magique reste magique en remplaçant chaque nombre par son carré, son cube ou autres puissances.

Il est bi-magique si les carrés forment aussi un carré magique.

Il est tri-magique s'il est bi-magique et que, en plus, les cubes forment aussi un carré magique.

Cette page n'est qu'un aperçu succinct sur les carrés multi-magiques.

Rendez-vous sur le site de Christian Boyer pour une revue exhaustive.

Carré ou bi-magique ?
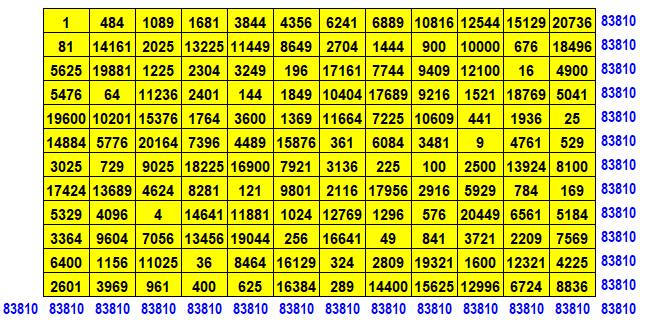
Un carré magique avec des nombres au carré a toutes ses sommes magiques. Les nombres utilisés sont des carrés distincts mais non nécessairement consécutifs. La grille formée par les nombres originaux portés au carré, n'est pas magique a priori.		Lorsque les nombres originaux portés au carré forment aussi un carré magique, le carré est dit bi-magique. En bref: un carré magique formé des nombres de 1 à n² dont le carré fait de ses carrés est aussi magique est un carré bi-magique.
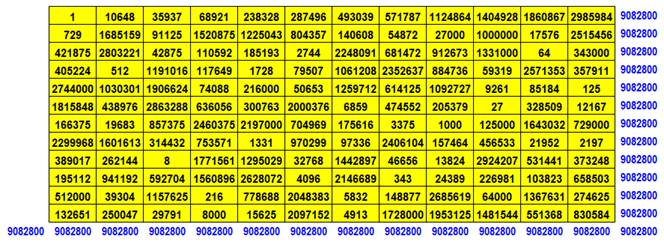
Quel est le plus petit ? Pas de construction possible pour les ordres inférieurs à 8. Le premier d'ordre 8 a été découvert en 1890. Le premier tri-magique fut trouvé en 2002. Il est d'ordre 12.	Quelle est la somme magique ? Pour le carré d'origine, la somme magique vaut (1/8 de la somme des nombres de 1 à 64 : Pour le carré au carré, la somme magique vaut (1/8 de la somme des carrés de 1 à 64):

BI-MAGIQUE ? Tentative

1	8	10	15
12	13	3	6
7	2	16	9
14	11	5	4

Ce carré est magique. En effet, la somme des nombres de chaque ligne est égale à la somme des nombres de chaque colonne, qui est égale à la somme des nombres de chaque diagonale.

	1	8	10	15	34
	12	13	3	6	34
	7	2	16	9	34
	14	11	5	4	34
34	34	34	34	34	34

	1	64	100	225	390
	144	169	9	36	358
	49	4	256	81	390
	196	121	25	16	358
434	390	358	390	358	442

Mais, si les sommes de carré présentent des similitudes, elles ne sont pas toutes égales. En fait, il n'existe pas de carrés bimagiques d'ordre 4. Il faut atteindre l'ordre 8 pour trouver le premier bimagique.

BIMAGIQUE d'ordre 8
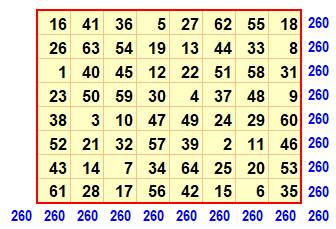
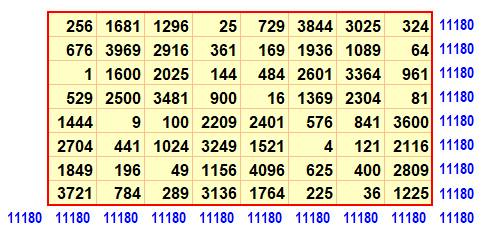
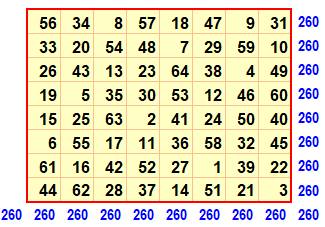
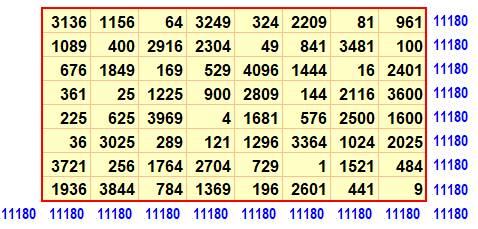
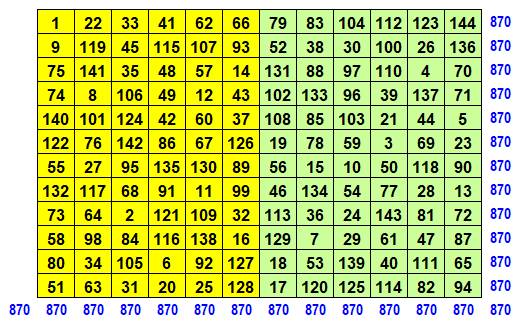
Nombre de 1 à 64 – Somme 260 = ½ n (n² + 1) Carré des nombres – somme 11 180 = n (n² + 1) (2n² + 1) / 6 Ce jeu de carrés bimagiques est dû à Pfeffermann

BIMAGIQUE d'ordre 9
Ce jeu de carrés bimagiques 9x9 est dû à Pfeffermann (1891)

BIMAGIQUE d'ordre 6
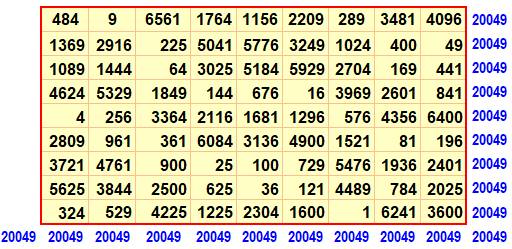
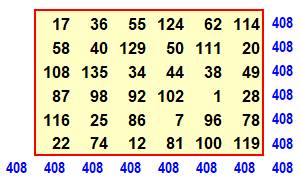
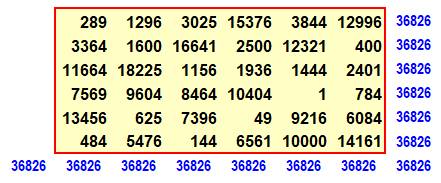
Ce jeu de carrés bimagiques 6x6 est dû à Wroblewski Composé de nombres distincts mais pas consécutifs.

TRIMAGIQUE d'ordre 12
Walter Trump publie ce carré tri-magique 12x12 en 2002.

Propriétés et bref historique

Le premier connu (G. Pfeffermann – 1890 – Allemand naturalisé français) était effectivement d'ordre 8, constante magique 260. Bensen et Jacoby conjecturent qu'il n'en existe pas d'ordre inférieur à 8, sauf trivial. Boyer et Trump le démontrent pour les carrés classiques utilisant les nombres de 1 à n². En 1891, Lucas puis Hendricks en 1998 ont montré qu'un carré bimagiques d'ordre 3 est impossible quel que soit la plage de nombres. En 1917 Henry Dudeney publie un carré bimagique, le second connu. En 1891, Pfeffermann trouve un carré bimagique d’ordre 9. Autour de 1900, Gaston Tarry, premier à construire un carré trimagique: un carré 128x128, donc de 16 384 cellules. En 1976, Benson et Jacoby confirment qu'il n'y a pas de carré bimagiques d'ordre inférieur à 8, ce qui fut prouvé par Boyer et Trump en 2002. En 1981, Chales Devimeux construit un quadri-magique 256x256. En 2002, Walter Trump publie un trimagique 12x12 En 2006, Christian Boyer: tous les carrés bi-magiques 9x9 construits avec la méthode Tarry-Cazalas sont une combinaison de 2 Sudokus. Prouvée en 2011. En 2014, Walter Trump and Francis Gaspalou ont calculé la quantité de carrés bimagiques 8x8: 26 158 848 dont 136 244 primitifs. Aujourd'hui, on connaît des carrés bimagiques pour tous les ordres de 8 à 64. Ils sont plus de 50 000 pour l'ordre 9. Le plus petit trimagique connu est d'ordre 12.

ENGLISH CORNER
A bimagic square is a magic square that also remains magic if all of the numbers it contains are squared. If in addition to being bimagic, the integers in the square can be raised to the third power and the resulting square is still magic, the square is then called a trimagic.

Suite	Carré pentamagique Carré magique avec nombres carrés Carré diabolique de Dürer Carré 5 x 5 Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Géométrie Humour Jeux Nombres consécutifs Nombres magiques - Index Pannumérique Rubriques débutants Propriétés du carré magique
Diconombre	Nombre 8
Sites	Liens vers les sites carrés magiques Bimagic square – Wolfram MathWorld Multimagie – Christian Boyer – Très complet – Tout ce que vous voulez savoir sur les carrés multi-magiques, y compris leurs valeurs Biographie de Georges Pfeffermann – Christian Boyer
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/Bimagiqu.htm