NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 29/01/2017

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

     

  CERCLE

 

Débutants

Géométrie

Types

 

Glossaire Géométrie

 

 

INDEX

 

Cercle

 

Géométrie

 

Neufs points

Ducci

Apollonius

Autres types

Monge

 

Sommaire de cette page

>>> Cercle égalitaire ou cercle de Ducci

>>> Calcul sur tableur

>>> Démonstration

 

 

 

 

 

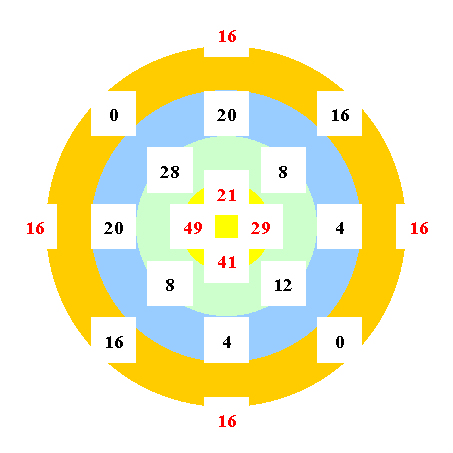
Cercle numérique de DUCCI

 

Sorte de cercles concentriques magiques comportant des nombres sur les circonférences.

 

 

 

CERCLE ÉGALITAIRE ou CERCLE DE DUCCI

 

Cercle de Ducci (1930)

 

*         Quatre nombres au centre (rouges).

*         Différence du plus grand au plus petit sur le cercle plus grand.

*         On recommence sur un nouveau cercle encore plus grand

*         Etc.

*         On aboutit toujours sur un quadruplet de mêmes nombres

*         Ici : 16 à la périphérie

 

Illustration

 

 

 

 

CALCUL SUR TABLEUR

 

Forme du tableur

 

a

b

c

d

a

Soit les 4 nombres a, b, c et d (on répète a).

25

32

41

52

25

Calcul a1 = ABS(25 – 32) = 7 ; idem pour a2 …

7

9

11

27

7

On recommence a2 = ABS(7 – 9) = 2.

2

2

16

20

2

0

14

4

18

0

14

10

14

18

14

4

4

4

4

4

On aboutit toujours à 4 nombres identiques.

  

 

 

Quelques exemples

 

1

2

3

4

1

1

1

1

3

1

0

0

2

2

0

0

2

0

2

0

2

2

2

2

2

 

1

3

6

10

1

2

3

4

9

2

1

1

5

7

1

0

4

2

6

0

4

2

4

6

4

2

2

2

2

2

 

2

4

8

16

2

2

4

8

14

2

2

4

6

12

2

2

2

6

10

2

0

4

4

8

0

4

0

4

8

4

4

4

4

4

4

 

25

30

40

60

25

5

10

20

35

5

5

10

15

30

5

5

5

15

25

5

0

10

10

20

0

10

0

10

20

10

10

10

10

10

10

 

10

100

1000

10000

10

90

900

9000

9990

90

810

8100

990

9900

810

7290

7110

8910

9090

7290

180

1800

180

1800

180

1620

1620

1620

1620

1620

 

 

 

 

 

 

 

 

 

DÉMONSTRATION

 

La démonstration passe par les étapes suivantes:

 

*         Démontrer que le plus grand nombre décroît en, au plus, 4 tours: si 10 est le plus grand nombre, il faudra, au plus, 4 x 10 = 40 tours pour atteindre 0.

*         S'il n'y a pas de 0 au départ, la décroissance est assez évidente.

*         Dans la mesure où le plus grand atteint 0, les trois autres sont aussi à 0.

*         Et, avant d'arriver à 0 tous les quatre, ils sont tous égaux.

*         Pour démontrer la décroissance vers 0, il faut considérer la présence de 1 à 3 zéros à côté du nombre le plus grand.

*         Avec 3 zéros, ils disparaissent en 3 étapes.

*         Avec 2 zéros, on examine les sous-cas: ils sont adjacents ou opposés.

*         Avec 1 zéro, on considère les trois autres nombres; s'ils sont tous différents ou non.

*         Un peu laborieux, mais de la pure scrutation des cas possibles. Plus facile à voir avec les dessins.

 

 

  

 

 

Suite

*    Nombre magique

*    Cercle d'Apollonius

*    Premiers en cercle

Voir

*    Cercle – Index

*    Géométrie – Index

*    Nombres magiques - Index

*    Itérations et cycles

*    Cercles

*    Carrés magiques

*    Nombres magiques

*    Grilles magiques

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Iteration/CercDucci.htm