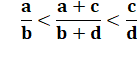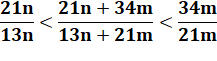|
|||||||||||||||||||||||||||||||||||
![]()
|
Le nombre 11 et sa magie La multiplication d'un nombre par 11 est assez
simple pour être réalisée mentalement. D'autres
propriétés extraordinaires vous attendent. Notamment
un tour de magie qui étonnera vos
amis: vous êtes capable d'additionner
dix nombres en moins de temps qu'il en faut pour les entrer dans la calculette! |
|
|
||
|
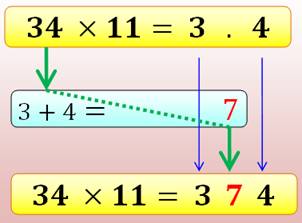
Pour multiplier un nombre de deux chiffres par 11:
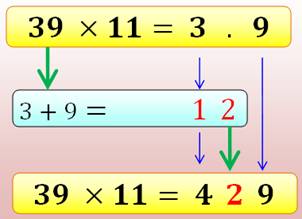
Dans le cas où, la somme
dépasse 9, faites fonctionner la
retenue comme pour une addition classique. |
Sans retenue
Avec retenue
|
|
|
Avec plus de chiffres,
appliquer la même méthode en cascade. Exemples sans et avec
retenue. En calcul mental, il est plus facile d'énoncer
les chiffres successifs que de nommer
le nombre complètement. |
123
x 11 = 1 / 1+2 / 2+3 / 3 = 1
3 5 3 789
x 11 = 7 / 7+8 / 8 + 9 / 9 = 7 / 15
/ 17 / 9 = 7+1 / 5+1
/ 7 / 9 = 8
6 7 9 |
|
Voir Divisibilité
par 11
|
|
||
|
Le retourné multiplié par 11 donne le résultat retourné du produit initial: N x 11 = M rN x
11 = rM rN
= retourné de N La condition pour que ça
marche: la somme de deux chiffres consécutifs doit être inférieure à 10
(sans retenue). |
Exemples 123
x 11 = 1 353 321
x 11 = 3 531 2
627 x 11 = 28 897 7
262 x 11 = 79 882 454
526 x 11 = 4 999 786 625
454 x 11 = 6 879 994 |
|
|
|
||
|
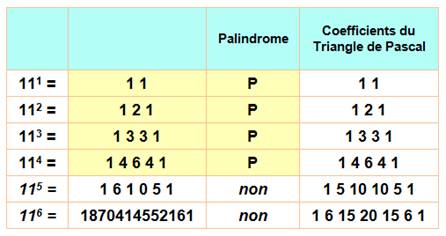
Les premières puissances de 11 sot palindromiques.
Ce sont même les coefficients du Triangle de
Pascal Lorsqu'apparaissent les
retenues, la forme palindromique est détruite. |
Autre manière de présenter ce résultat
|
|
|
|
||
|
|
||||
|
Explication |
Exemple |
Formulation |
||
|
Demandez à quelqu'un de
choisir deux nombres entre 1 et 20 (ce qui facilitera les calculs). |
1 6 2 13 |
n |
m |
|
|
Demandez à cette personne d'additionner
les deux nombres. Continuez d'additionner les
deux derniers nombres, jusqu'à obtenir dix résultats. Vous pouvez mettre un numéro de ligne pour
faciliter le compte. La calculette est conseillée, car le résultat
doit être juste, évidemment. |
3 19 4 32 5 51 6 83 7 134 8 217 9 351 10 568 |
n n 2n 3n 5n 8n 13n 21n |
+ m + 2m + 3m + 5m + 8m + 13m + 21m + 34m |
|
|
Vous pariez que vous connaissez
instantanément la somme de ces nombres. Comment faites-vous? Vous notez mentalement le 7e
nombre et vous le multipliez par 11. C'est la réponse. |
S = 134 x 11 = 1 474 |
S = 55n S = 11 (5n |
+ 88m + 8m) |
|
|
Vous avez sans doute reconnu
la suite de Fibonacci. Le rapport entre deux
nombres successifs de cette suite tend vers le nombre d'or 1, 618… |
1, 1, 2, 3, 5, 8, 13 … |
|||
|
Demandez à votre interlocuteur
de diviser le 10e nombre par le 9e. Vous êtes capable de lui
donner les trois premiers chiffres: 1,61. Note: si l'écart est
assez grand entre n et m, le 8 est présent (1,618). C'est le cas : si n = 1 pour m > 1; si n = 2 pour m > 3; si n = 3 pour m > 4 ; si n = 4 pour m > 6; etc. si n = k pour k > (m + m/2 + 1)entier Pour un écart très grand entre n et m, on passe à
1,619. Ex: n = 1 et m > 42; n =
2 et m > 84; etc. |
R = 568 / 351 = 1,6182 |
Inégalité (propriété)
Voir Fractions Application
|
||
|
La magie continue à marcher au-delà
de 20 bien entendu. Exemple avec n =
123 et m = 456. |
|
|||
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()