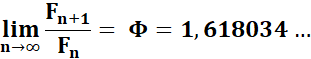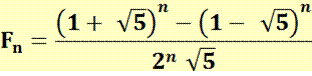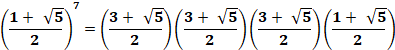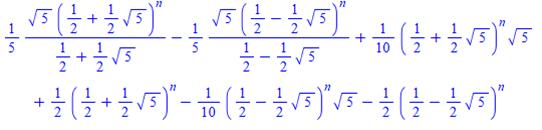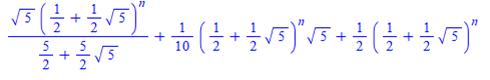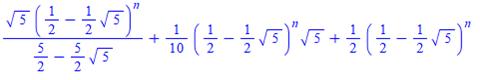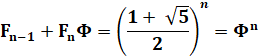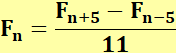|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SUITE DE FIBONACCI Propriétés Revue des
principales propriétés des nombres de Fibonacci. |
|
|
||
|
Chaque
terme est la somme des deux précédents. Chaque
terme est la différence entre ses deux voisins. |
Fn+1 = Fn + Fn–1 Fn = Fn+1 – Fn–1 |
|
|
Six
nombres dont la somme est 13. À partir du troisième, chacun est la somme des
deux précédents. Le dernier est le quadruple du premier. Valeur des deux
premiers nombres ? |
|
|
||
|
Rapport: le nombre d'or |
|
|
|
Calcul direct d'un nombre de
Fibonacci (formule de Binet) >>>l |
|
|
|
Somme |
Fi +
j = Fi+1 . Fj + Fi . Fj–1
|
|
|
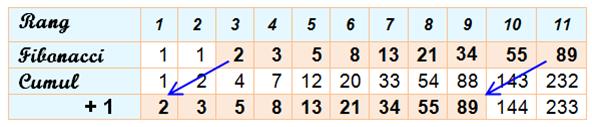
Cumul |
Fn+2 =
F1 + F2 +...+ Fn + 1 |
|
|
Fn
– 1 = Fn-1 + Fn-3 + Fn-5 + … F3 ou 2 |
||
|
Cumul pondéré |
nFn+2 – Fn+3 = F1 + 2F2
+...+ nFn – 2 |
|
|
F12 = 144 = 12² Seul Fibonacci carré, hors 1. |
||
|
Divisibilité >>> |
Si
n divise
m, alors
Fn divise
Fm |
|
Divisibilité par 11 >>> |
|
|
Divisibilité par 29 >>> |
Fn + Fn+1 + … + Fn+13 |
|
Trois Fibonacci consécutifs
sont premier entre eux >>> |
(Fn-1, Fn) = (Fn-1, Fn+1)
= (Fn, Fn+1) = 1 |
|
Le PGCD de deux Fibonacci
est égal au Fibonacci d'indice égal à ce PGCD >>> |
(Fn, Fm) = F(n, m) |
|
Quatre
Fibonacci consécutifs forment un triplet
de Pythagore |
Fn+2 . Fn+3 – Fn . Fn+1 2 . Fn+1 . Fn+2 Fn . Fn+3 |
Démonstration Fibonacci et triplets de Pythagore
|
Les quatre
nombres successifs de Fibonacci: x, y, x + y, x + 2y Vérification que
a² = b² + c²: a = (x + y) (x +
2y) – xy => a² = x4 + 4x3y + 8x2y2
+ 8xy3 + 4y4 b = 2y (x + y)
=> b² =
4x2y2 + 8xy3 + 4y4 c = x (x + 2y)
=> c² = x4
+ 4x3y + 4x2y2 |
|
Fibonacci entre eux |
Fn
– Fn-1 – Fn-2 = 0 |
|
Carrés entre eux |
Fn2
– 2Fn-12 – 2Fn-22
+ Fn-32 = 0 |
|
Cubes entre eux |
Fn3 – 3Fn-13
– 6Fn-23 + 3Fn-33
+ Fn-4 = 0 |
|
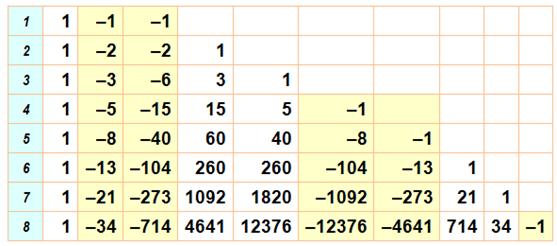
Généralisation Puissances entre elles Triangle de Fibonacci
=> |
Table Elle donne les coefficients (dits de
de Fibonacci) des expressions du type de celles-ci-dessus.
Calcul Factorielle
de Fibonacci: n!F = 1 x
1 x 2 x 3 x 5 x 8 x … x Fn Exemple: 5!F = 2 x 3 x 5
= 30 6!F = 2 x 3 x 5
x 8 = 240 Les suivantes: 3120, 65520, 227680,
122522400, 10904493600, … Coefficients du triangle
Voir
similitude avec les Coefficients
du binôme |
|
Carré et produit |
Fn2
= Fn–1 . Fn+1 + (–1)n–1 Voir Démonstration |
|
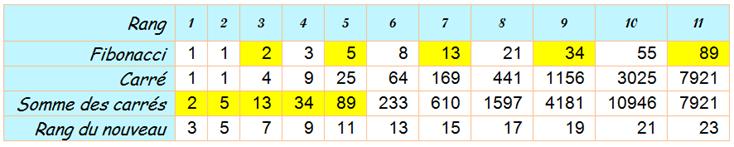
Somme de carrés |
F12
+ F22 +…+ Fn2 = Fn . Fn+1 |
|
Carré généralisé (G est la
suite de Fibonacci dont les valeurs de départ ne sont pas précisées) |
Gn2 = Gn-1 . Gn–2
+ e (G22
– G12 – G1G2) ( avec e = 1 ou -1) |
|
Somme de carrés |
Fn2 + Fn+12
= F2n+1 |
|
Différence de carrés |
Fn+22
– Fn+12 = Fn . Fn+3 |
|
Lien avec la suite de Lucas |
Ln
= Fn-1 + Fn+1 Ln
= F2n / Fn |
|
On ne sait s'il existe une infinité de Fibonacci premiers. PGCD = Plus grand commun diviseur |
Fn
et Fn+1 sont premiers entre eux. PGCD ( Fi , Fj ) = FPGCD
(i, j)
Réciproque
non valable. Le plus
petit contre-exemple est F19 = 4181 = 37 x 113.
|
|
Veut dire:
quelque soit n, il existe … |
Si j divise i alors Fj
divise Fi
|
Voir Sommation
des nombres de Fibonacci
|
Fibonacci et nombre d'or |
Exemple
avec F6 = 8 et F7 = 13
|
|
Démonstration
avec la formule de Binet, en posant
Le
membre de gauche
devient (en multipliant les termes en puissance n – 1 pour le passer en
puissance n)
En
développant
En calculant les trois termes en A
Qui vaut
En calculant les trois termes en B
Qui vaut
Bilan
|
|
|
|
||
|
|
Fn+2 =
F1 + F2 +...+ Fn + 1 |
|
|
Voir Addition magique |
||
|
|
F2n+1 = F1
+ F2 + F4 + F6
... +
F2n |
|
|
|
||
|
|
||
|
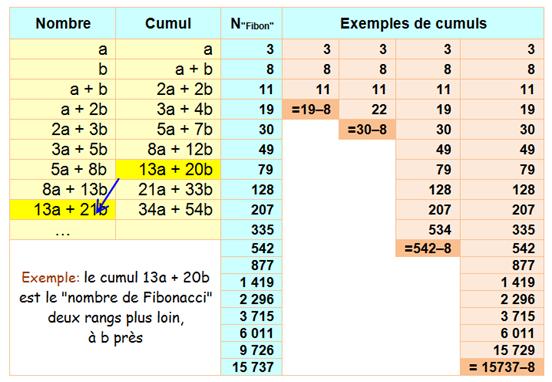
Exemple 3
+ 8 + 11 = 22 = 30 – 8 |
|
|
Voir Somme
magique (tour de magie)
|
|
||
|
|
|
|
|
|
||
|
Un
nombre de Fibonacci est égal à 1/11e de la différence entre les
deux nombres de Fibonacci éloignés de cinq rangs de part et d'autre. Exemple F10
= 55 F15
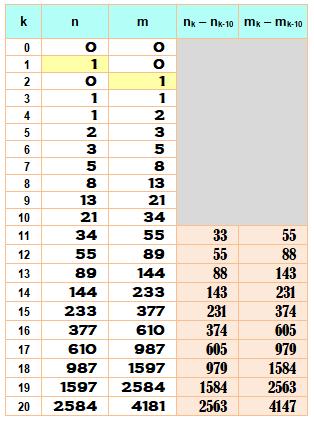
– F5 = 610 – 5 = 605 = 11 x 55 Tableau Le
tableau commence par deux nombres quelconques n et m FK = n FK+1 = m FK+2 = n
+ m FK+3 = n
+ 2 Etc. Les
deux colonnes de droites montrent la différence entre deux Fibonacci
quelconques séparés de dix rangs. Tous les nombres dans la parie rose sont
divisibles par 11. |
pour n>10 Fk+10
– Fk = 11. Fk+5
|
|
|
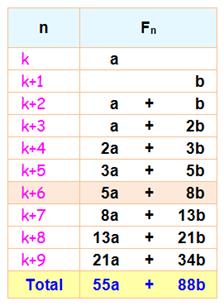
La
somme de dix nombres successifs est égale à 11 fois le septième (k+6) terme. En prenant deux nombres de Fibonacci a et b et leur
successeurs jusqu'au rang 9, la somme des termes en a donne 55a et celle des
termes en b donne 88b, deux valeurs divisibles par 11. S
= 55a + 88 b = 11 (5a + 8b) Notez que la valeur entre parenthèse est un nombre de
Fibonacci: S
= 11 Fk+6 |
Fk
+ Fk+1 +...+ Fk+9 = 11. Fk+6
|
|
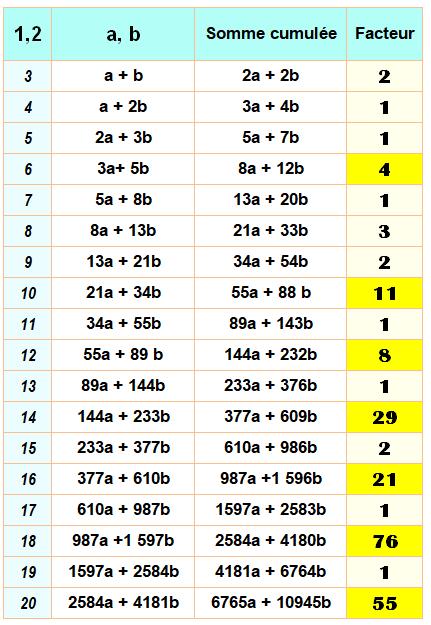
Récapitulatif de la divisibilité des sommes de k Fibonacci successifs
Ex:
la somme pour k = 14 est divisible par 29
1+1+2+3+5+8+13+21+34+55+89+144+233+377 = 986 = 29 x 34
|
|
||
|
Démonstration
|
sont premiers entre eux. F0
= 0 F1
= 1 PGCD (F0, F1) = 1 PGCD (Fn , Fn+1) = 1 Hypothèse Fn+1
= Fn + Fn-1 On prend la précaution de noter que la
suite est croissante. Fn+1 = 1x Fn
+ Fn-1 Fn = 1x Fn-1
+ Fn-2 En couleur, les termes qui se propagent
dans l'algorithme d'Euclide PGCD
(Fn , Fn+1) = PGCD (Fn-1 , Fn) PGCD
(Fn , Fn+1) = PGCD (Fn-1 , Fn) =
PGCD (Fn-2 , Fn-1) = … =
PGCD (F0, F1) = 1 La relation supposée est vrai pour n+1,
elle est vraie pour tout n. |
|
|
|
PGCD ( Fi , Fj ) = FPGCD
(i, j) Exemple: F6 = 8 et F9 = 34 PGCD (6,9) = 3 et
F3 = 2 PGCD (8, 34) = 2 |
|
|
|
||
|
|
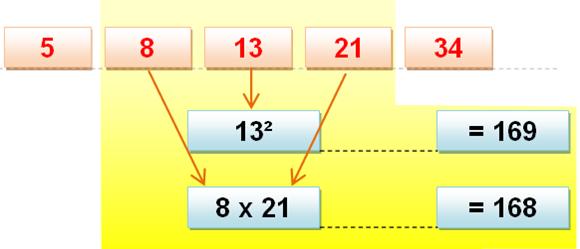
Relation de Simson Fn2
= Fn–1 x Fn+1 + (–1)n–1 |
|
|
|
||
Voir
Paradoxe de Lewis Carroll
|
|
|||
|
|
Fn ² + Fn+1 ² = F2n+1 Note: n + n + 1 = 2n + 1 |
||
|
Exemple: 5² +
8² = 25 + 64 = 89 qui est le Fibonacci de rang 2 x 5 + 1 = 11. |
|||
|
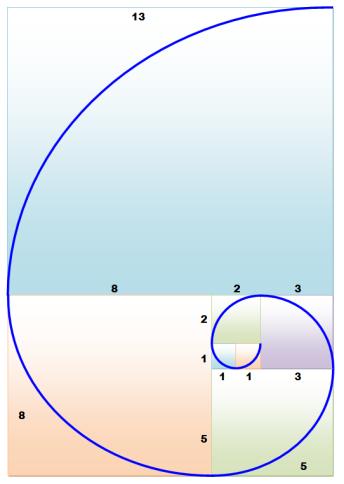
Métaphore de l'escargot qui agrandit sa
coquille au fur et à mesure de sa croissance: Carré unité, puis un autre carré unité. Résolution: voir plus grand ! 1, 1, 2, 3, 5, 8, 13, 21…
|
|
||
|
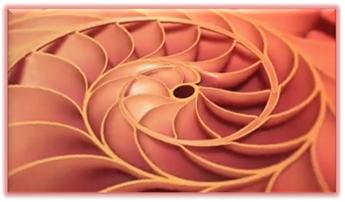
Spirale d'or Spirale logarithmique dont le facteur de croissance est le
nombre d'or. Elle est auto-similaire (fractale). |
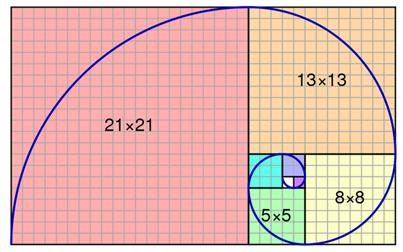
Spirale de Fibonacci Construite par quarts de cercle tangents aux côtés des
carrés dont les côtés sont les nombres successifs de Fibonacci. Bonne approximation de la spirale d'or. |
||
Voir Spirale logarithmique / spirale du pentagone
Présentation de la spirale de
Fibonacci avec quadrillage
|
|
|||
|
/ |
|
|
|
|
/ |
|
|
|
|
F10 |
|
||
|
F12 |
|
||
|
F12 F 13 F14 |
144 233 377 |
|
|
|
F22 |
17 711 |
|
|
|
F31 |
1 346 269 |
|
|
|
F74 |
1 304 969 544 928 657 |
|
|
|
|
1/89 = 0, 012359550561797… |
|
|
|
Énigme
Six
nombres dont la somme est 13. À partir du troisième, chacun est la somme des
deux précédents. Le dernier est le quadruple du premier. Valeur des deux
premiers nombres ? Solution On
écrit les six nombres en fonction de leurs relations (bleu).
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/FiboProp.htm |
![]()