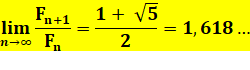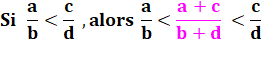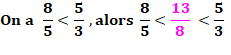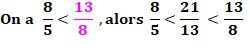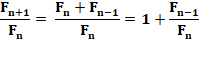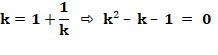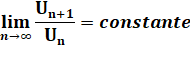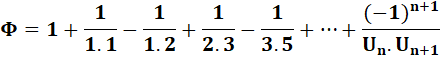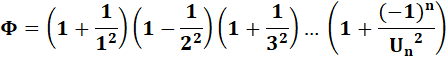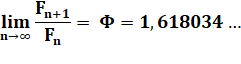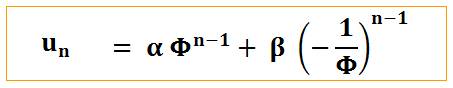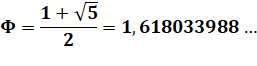|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombre d'or et ses relations avec la suite de Fibonacci
|
Nombre d'or comme limite du rapport entre
nombres de Fibonacci
|
Propriété Le rapport entre deux nombres de Fibonacci successifs tend vers le
nombre d'or lorsque ces nombres tendent vers l'infini.
|
||
|
Explications Prenons trois nombres de Fibonacci successifs comme
3, 5 et 8 et leurs deux rapports: 5/3 = 1,666… et 8/5 = 1,6. Ces deux rapports sont décroissants et cette
propriété est valable pour la suite de Fibonacci. On a ainsi deux rapports tels que a/b < c/d. Dans ce cas, on sait trouver une fraction
médiane:
Avec les nombres de Fibonacci:
Les suivants, en reprenant la fraction médiane que nous venons
d'obtenir:
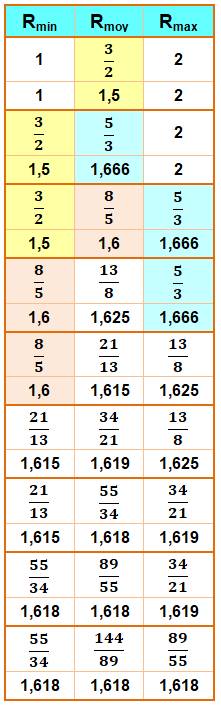
Convergence Progressivement, la fraction médiane est enfermée
dans un intervalle qui se réduit. Elle converge vers 1, 618 …, le nombre
d'or. Le tableau montre (code couleur) la naissance et
la destinée de chacun des rapports. Une fraction naissante (au centre)
devient soit la plus petite des deux lignes suivantes ou la plus grande. |
|
|
|
Convergence vers le nombre d'or Nous savons que Fn+1 / Fn converge vers une
constante k, mais quelle est sa valeur ?
|
De sorte qu'en tendant vers l'infini, on a:
Équation
dont l'une des racines est le nombre d'or. |
|
![]()
|
|
||||||||||||||||||||||||||||
|
Puissance
de Phi et Fibonacci en formule – Suite d'or
Voir Puissances de Phi Φ
n = Φ n-1 + Φ n-2 = a Φ + b ou a et b sont des
suites de Fibonacci. La
suite des nombres de Fibonacci est la
seule suite ayant les deux propriétés:
Développement
de Phi et Fibonacci: Si
on calcule Φ avec le développement de sa fraction
continue: Φ = 1+ 1/ (1+
(1/ ...
On
retrouve au numérateur et dénominateur la suite de Fibonacci. Ces formes sont
appelées les réduites du nombre d'or. |
||||||||||||||||||||||||||||
Voir Tour
de magie exploitant cette propriété
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le
rapport entre deux nombres de
Fibonacci consécutifs tend vers le nombre d'or.
Le
nombre d'or sévit également avec la cousine de la suite de Fibonacci, la
suite de Lucas:
Exemples
Nombre
d'or = 1,6180339887… La
vitesse de convergence du rapport de deux nombres successifs vers le nombre
d'or est quasiment identique en Lucas comme en Fibonacci: < 1/ 1 milliard après 25 termes. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Voir Développements
et exemples
Merci à Jamila B. pour ses remarques
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrFibo.htm |
![]()