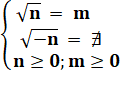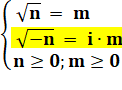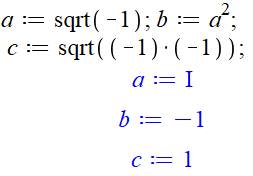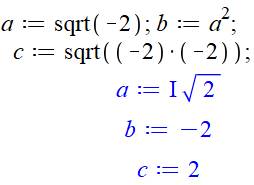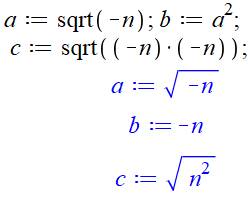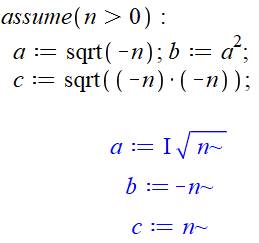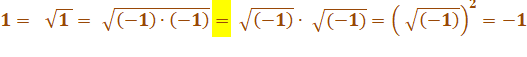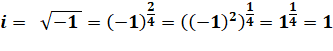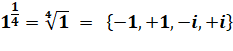|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
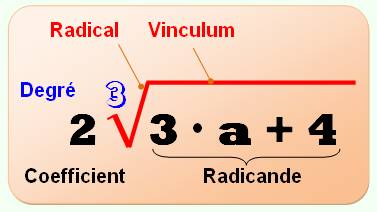
RADICAL et nombres complexes
Symbole classique de la racine
d'un nombre ou d'une expression. La valeur sous radical (radicande) est
positive et le résultat de cette opération est positif. Attention, dans le monde des nombres
complexes son usage est plus délicat. Certaines opérations sont
interdites. Les mots "radicande" et "vinculum"
sont peu usités. "Degré" ou "index" sont peu
employés: on dit racine énième ou racine d'ordre n. |
Voir Radical
d'un nombre entier
Définition
|
|
|
|
||||
|
RADICAL |
Réels |
Complexes |
||
|
Effet de l'opération radical |
Positif => Positif |
Positif => Positif Négatif => i · Positif* * Perte de
symétrie, pas sans conséquence |
||
|
Réponse |
|
|
||
|
Convention |
|
|
||
|
Équations: deux racines.
L'opération radical ne conserve que la racine positive |
|
|
||
|
Exemple avec 1 |
|
|
||
|
Exemple avec 4 |
|
|
||
|
Composition des produits |
|
|
||
|
Attention: égalité
impossible en complexe ! |
La loi
sur les produits:
n'est
généralement valable que si les
nombres a et b sont positifs. |
Du fait de la perte de symétrie, la loi sur les produits n'est pas
valable avec les nombres négatifs.
|
||
|
Conclusion |
Le radical signifie racine carrée positive d'un
nombre positif. |
Le radical signifie racine carrée positive (complexe). Du fait de la perte de la loi sur les produits, prudence
avec l'emploi du symbole radical avec les nombres négatifs. Voir ci-dessous, le procédé de calcul à retenir. |
||
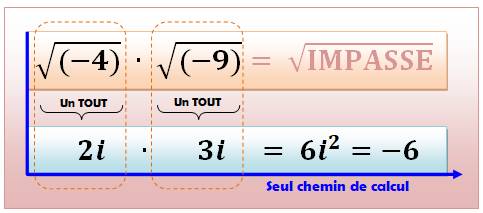
Procédé de calcul avec des racines de nombres négatifs
![]()
Explications détaillées
|
|
|||
|
|
Il signifie racine carrée positive du nombre entier n. Aucun nombre n'est négatif. |
|
|
|
Racine
carrée négative d'un nombre |
Il est pourtant vrai que le nombre négatif (–2) est une solution de x² = 4 |
|
|
|
Racines d'une équation |
On dit que 2 et –2 sont les racines de l'équation x² = 4 |
|
|
|
Composition
des radicaux |
Produit de deux racines carrées avec des nombres
positifs sous les radicaux. Rappel: nous sommes
dans le monde des nombres réels
positifs. |
|
|
|
Attention |
Si le
produit sous le radical est positif, le calcul est possible. Le produit de racines de nombres négatifs est
impossible. |
|
|
|
|
|||
|
Radical avec –1. |
Par convention, on pose i² = –1. La racine carrée de –1, par convention, est égale
au nombre imaginaire i. |
|
|
|
Racine
négative. |
Comme pour les réels, on a une équation avec deux
racines. |
|
|
|
Composition
sous radicaux: |
La multiplication avec un produit positif sous le
radical est toujours permise. |
|
|
|
Produit
de radicaux |
Par convention, l'opération radical ne conserve que
la racine positive accompagnée de "i".
|
|
|
|
Commentaires – Calcul numériques |
|
|||
|
Composition interdite ? |
Prudence, avec les nombres complexes, la composition des produits n'est pas possible. |
|
||
|
Racine de produit |
Calcul avec nombres. |
|
||
|
|
Calcul avec imaginaire i. |
|
||
|
|
Calcul avec racine directement. |
|
||
|
Produit de racines |
Ici, un seul calcul possible. |
|
||
|
Bilan |
Certains calculs semblent erronés. L'artefact provient
du fait que le passage au carré produit deux valeurs et on en choisit une
seule avec la racine carrée. |
Le mystère provient du fait que:
|
||
|
|
|||
|
En bref |
Les logiciels conservent bien la racine positive
dans tous les cas. Ils confiment de ce fait l'inégalité entre
produit de racines et racine du produit. |
||
|
En haut Avec –1 et –2, résultats différents confirmés. En bas, avec nombre quelconque À gauche et deuxième ligne, le logiciel ne sait
pas calculer. Il ne peut pas décider,
car il existe deux racines, la positive et la négative. À droite, on commence par déclarer que les
valeurs seront positives. Le logiciel calcule. Le résultat est suivi d'un
tilde signifiant la présence d'une hypothèse. |
|
|
|
|
|
|
||
Anglais: to assume: supposer/ sqrt est l'abréviation de squarre root, racine carrée
Résumé: nombres complexes
|
Écrire des nombres négatifs
sous radicaux induit automatiquement que nous sommes dans le monde des
nombres complexes.
Voir Commentaires sur la légitimité
d'écrire racine de –1 Il est vrai qu'un des buts de l'introduction des
nombres complexes est de disposer de toutes les racines d'un nombre, qu'elles
soient réelles ou imaginaires. Il est donc naturel de penser que parler de la
racine dans le monde des complexes fait automatiquement penser à toutes les racines. |
|
|
||
|
En
écrivant ceci, on fait une erreur. |
|
|
|
Ceci est
correct |
|
|
|
Ceci est
aussi correct |
|
|
|
Mais,
ceci, non ! |
|
|
Merci à Pierre
Menissier pour m'avoir rappelé ce paradoxe avec
racines de – 1
|
Un autre
paradoxe |
|
|
Explication |
Ici aussi, la suite des calculs ignorent toutes
les possibilités des racines. Le problème est d'avoir élevé au carré, créant de
facto deux solutions que la prise de racine carrée devrait prendre en compte. |
![]()
Notation symbolique de i = racine de –1 – Légitimité ?
|
Racine des nombres négatifs: la
notation
Autres notations: en électronique
le i est remplacé par j pour ne pas confondre avec i comme intensité. En calcul symbolique sur
ordinateur, le i devient majuscule I. Définition
anglaise: a
complex number is a number of the form a + ib where a, b Quelques définitions sur Internet
Encyclopédie de
référence américaine:
The complex numbers are the field Conclusion: on ne se privera pas d'employer cette notation Intégrant l'enseignement supérieur, il sera toujours temps de pointer les
subtilités de l'emploi du radical. |
![]()
|
Suite |
|
|
Terminale |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()