NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/05/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Théorie mathématique			Glossaire Carrés magiques
INDEX Carrés magiques Calculs Jeux	Construction	Méthode d'Euler	Méthode diagonale	Symétrie
	Latin	Gréco-latin	Échelle alternée	Parallélogramme
	Tapis (prog)
		Sommaire de cette page >>> Parallélogramme vectoriel >>> Parallélogramme et carré magique 3x3 >>> Modèle avec des complexes

Mathématiques des Carrés Magiques

Le carré 3x3 et le parallélogramme

En 1997, Lee Sallows publie un article dans lequel il fait part de son émerveillement à la découverte d'une correspondance presque évidente entre un carré magique d'ordre 3 et le parallélogramme.

Le même article fait état de sa découverte d'un carré magique de carrés 3x3 presque parfait.

Parallélogramme vectoriel
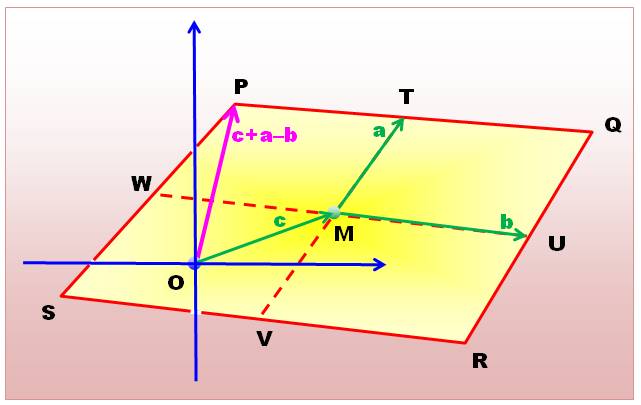
Un parallélogramme PQRS. Ses sommets et les points milieux des côtés (T, U, V, W) sont définis par des vecteurs issus d'une origine externe au plan du parallélogramme.
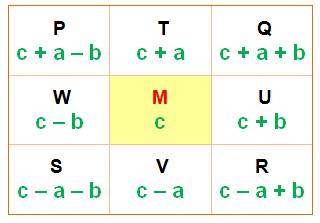
Définition des 9 points. Par construction du parallélogramme et de ses points milieux, deux points diamétralement opposés sont symétriques. Autrement-dit, les nombres pris par 3 le long d'une ligne sont en progression arithmétique.

Parallélogramme et carré magique 3x3

Formules de Lucas pour le carré magique 3x3

c – b	c + a + b	c – a
c – a + b	c	c + a – b
c + a	c – a – b	c + b

Correspondance avec les coordonnées des points du parallélogramme.

On retrouve exactement la correspondance avec les progressions arithmétiques dans le carré magique 3x3 >>>

W	Q	V
R	M	P
T	S	U

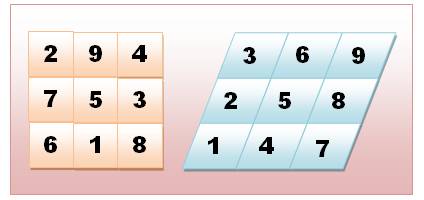
Exemple de correspondance

Notez les progressions arithmétiques sur le parallélogramme: de +3 en horizontal et +1 en oblique.

Elles sont nécessairement différentes, sinon le carré serait bien banal.

Théorème de Sallows

Tout parallélogramme définit un carré magique d'ordre 3 unique et réciproquement.

Ou d'une façon générale: pour tout parallélogramme du plan, il lui correspond une classe d'équivalence unique de 8 carrés magiques complexes d'ordre 3, et pour toute classe d'équivalence de 8 carrés magiques complexes d'ordre 3, il lui correspond un parallélogramme unique dans le plan.

Modèle avec des nombres complexes
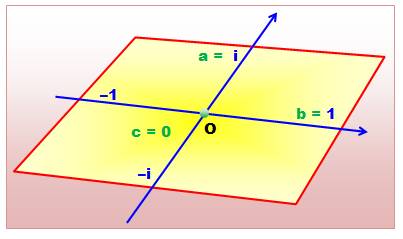
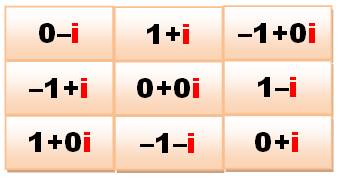
Lee Sallows ne s'arrête pas là. Il imagine son parallélogramme dessiné dans le plan complexe (au passage, devenant un carré), et il simplifie le plus possible les coordonnées. Nous sommes donc dans le plan complexe et les coordonnées des points milieux sont en 1, -1, i et –i. D'une certaine façon quatre représentations de l'unité.
En reportant les coordonnées à leur place dans le carré magique, on obtient une représentation reflétant toute la symétrie interne au carré magique d'ordre 3.
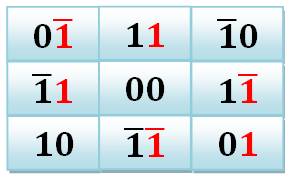
Encore mieux, en adoptant ce codage. "Could anything be more natural, or poetic?" Se peut-il que quelque chose soit plus naturel ou poétique se demande Lee Sallows en conclusion de son article.

Suite	Carré à échelle alternée – Vers les carrés de Franklin Carrés magiques – Index Construction matricielle des carrés magiques Carré latins et constructions de carrés magiques Relations mathématiques dans le carré3x3 Relations mathématiques dans le carré 4x4 Relations mathématiques dans le carré 5x5 Symétries dans le carré magique
Voir	Jeux – Index Jeux de nombres – Index Jeux numériques – Index Rectangles magiques
Sites	Voir page spéciale The lost Theorem – Lee Sallows – 1997 – Référence pour la rédaction de cette page
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/Parallel.htm