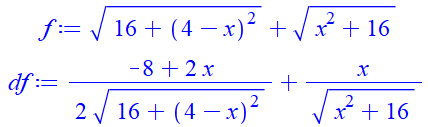|
|||||||||||||||||||||||||||||||||
![]()
|
Fonctions et leurs minimums Exemple simple de résolution
conduisant à la notion de minimum (donc de dérivée,
sans la nommer) sur une fonction. |
|
|
||
|
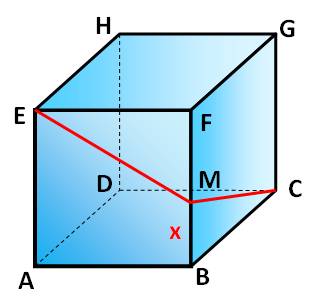
Problème Un cube
de 4 cm de côté. Une
fourmi part du point E pour atteindre le point C. Elle
passe par le point M situé à une disatnce x du point B. On se
propose de déterminer la position u point M pour minimiser le parcours de la
fourmi. Questions Si f(x) représente la longueur EM + MC, quelle
sont les valeurs possible de la variable x. Donner l'expression de f(x). Avec une calculatrice estimer le minimum de f(x)
et justifier à partir du patron du cube. |
|
|
|
Observations On commence
par faire travailler notre intuition. Le trajet
EMC (imaginez la fourmi qui se promène) traverse deux carrés absolument
identiques. Imaginez que la fourmi reparte dans l'autre sens: CME. Le trajet
est symétrique. Il n'y a pas de raison pour que le trajet
sur l'un des carrés ou l'autre soit différent. Pour que ce soit possible, il
faut que M soit le milieu de BF. Alors, on
a le même trajet sur chacun des deux carrés. |
||
Voir Fourmi sur
parallélépipède (ou pavé)
|
|
||
|
Ensemble des valeurs possibles pour
x |
Le point
M se déplace de B à F, une arête du cube qui mesure 4 cm. La
variable x peut prendre toutes les valeurs de x = 0 à x = 4. |
|
|
Calcul des longueurs EM et MC Expression de f(x) |
Avec le théorème
de Pythagore:
S'agissant
d'une somme de racines, il n'est pas possible simplifier. |
|
|
|
||
|
Observation On avait
remarqué la nécessité d'une symétrie pour les deux carrés traversés. On a ici
pour f(x), une somme de deux termes qui se ressemblent. Comment les rendre
totalement semblable. Oui! en
prenant: x = 2. |
||
|
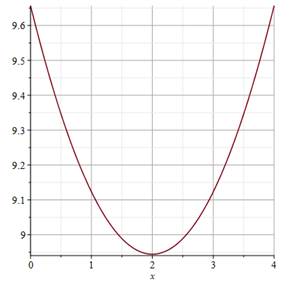
Graphe de la fonction On sait
que x varie de 0 à 4. Je trace
la courbe avec la calculette. Je note
un minimum pour x = 2 et y voisin de 8 Je
vérifie pour x = 2:
Pour x =
1,99 => f(x) = 8.944289 Pour x =
2 => f(x) = 8.944271 Pour x =
2,01 => f(x) = 8,944289 La valeur
x= 2 est bien l'abscisse du point pour f(x) minimum. |
|
|
Recherche systématique avec tableur ou calculatrice
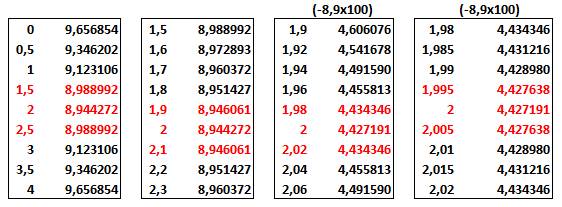
Sur
les tableaux de droite, on a retiré 8,9 et on a multiplié par 100 pour mieux
observer le passage par le minimum
|
|
||
|
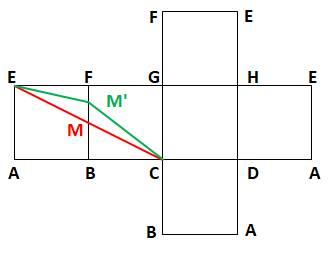
On
dessine le patron
du cube en respectant la notation des sommets. On
représente le trajet AMC quelconque (vert) et le trajet AMC avec M au milieu
de FB (rouge) La ligne
droite est le plus court chemin d'un point à un autre. C'est bien le trajet rouge qui représente une longueur minimum. |
|
|
|
On
a recherché le passage par un minimum "à la main". Nous
apprendrons qu'il existe un outil pour atteindre cet objectif très
précisément, c'est la dérivée. Dans
notre cas, elle n'est pas simple:
Et
son passage à 0 est obtenu pour x = 2, confirmant la recherche faite
ci-dessus. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()