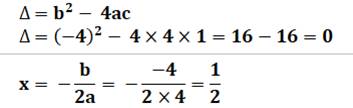|
|||||||||||||||||||||||||||||||||
![]()
|
ÉQUATIONS du DEUXIÈME DEGRÉ Familiarisation avec la tangente Approche de la tangente à
une parabole. |
|
|
||
|
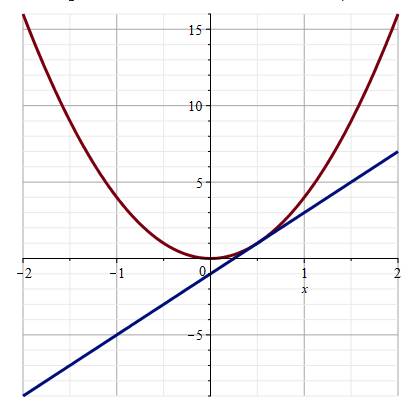
Énoncé Une
droite: y = 4x – 1 Une
parabole: y = x² 1) Faire la figure: 2) Commentez les points communs; et 3) Résoudre l'équation |
|
|
|
|
||
|
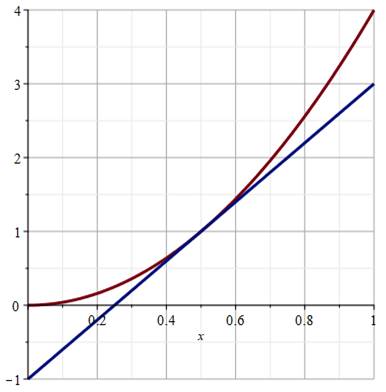
Le graphe
précédent montre une intersection aux environs de x = 0,5. On zoome
sur la zone de connexion. Finalement ce n'est pas un point d'intersection,
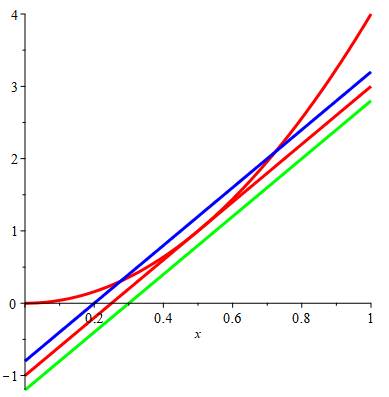
mais un point de tangence. Explications Avec une droite de même pente, mais décalée vers
le haut (droite bleue: y = 4x – 0,8); alors cette droite coupe la parabole en
deux points Avec une droite de même pente, mais décalée vers
le bas (droite verte: y = 4x – 1,2); alors cette droite ne coupe plus la
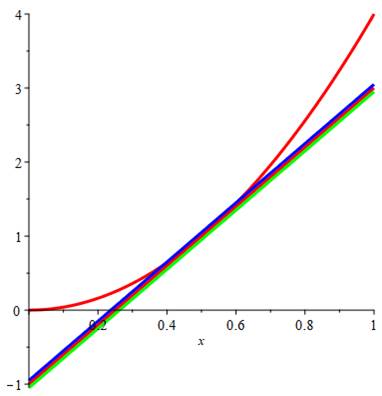
parabole. En diminuant l'écart, la droite bleue et la
droite rouge se rapprochent jusqu'à se confondent. Les deux points de la
droite bleue deviennent un point double. On dit qu'il y a tangence. Ce point se trouve (lecture sur le graphique) en y = 1 et x = 0,5 Voyons nos deux équations: y = 4x
– 1 y = 4x²
= 4 x 0,5 ² = 4 x 0,25 = 1 |
|
|
|
|
|||
|
Équation Avec tout du même côté |
4x² = 4x – 1 4x² – 4x + 1 = 0 |
||
|
Méthode par factorisation |
4x² – 4x + 1 = 0 (2x – 1)² = 0 2x – 1 = 0 x = 1/2 |
(ax + b)² = a²x² + 2abx
+b² a² = 4 => a = 2 b = -1 ou +1 Lever de doute avec – 4 x => b = -1. |
|
|
Méthode générale Discriminant Il est nul, racine double |
|
||
Voir Résolution
des équations du deuxième degré
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()