NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/04/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Exercices de calculs
Débutants Équations	Initiation aux fonctions			Glossaire Général
INDEX Enseignement Équations Calcul	Tangente	Carrés, périmètre et aire	Fermier et pommes de terre
	Aire lettre H	Parcours sur un cube	Cylindre déformable
	Lycée – Seconde	Sommaire de cette page >>> Lettre H >>> Aire de la lettre H >>> Aire à ne pas dépasser >>> Analyse du signe >>> Choix

ÉQUATIONS du DEUXIÈME DEGRÉ

Initiation

Exemple d'approche avec le calcul de l'aire dans la lettre H.

Lettre H
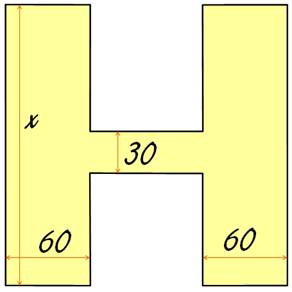
Énoncé La lettre H est inscrite dans un carré dont le côté mesure x cm, avec x 130 cm Quelles est la valeur de x qui minimise la partie blanche à évider sans dépasser 2 200 cm² ? 1) Calculer l'aire A(x) 2) On veut une aire blanche au moins égale à 2 200 cm². Écrire l'inéquation A(x) 2 200 cm² en factorisant. 3) Valeur de x ?
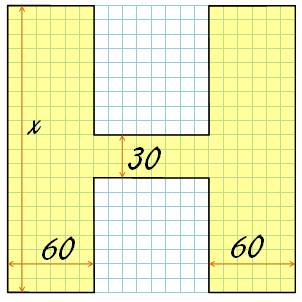
Familiarisation Pour tout problème, mieux vaut s'attarder un peu sur l'énoncé et se familiariser avec les questions posées. On refait la figure avec du papier quadrillé: 1) Le H est inscrit dans un carré, le côté vertical vaut x; le côté horizontal aussi. 2) Si on diminue la valeur de x les pattes du H vont se toucher et après ce n'est plus un H. On atteint ce cas pour x = 2 x 60 = 120. Donc x est supérieur à 120 pour former un H. L'énoncé dit 130, mais on n'avait même pas besoin de cette donné. 3) La figure quadrillée donne une zone blanche de 13 600 cm². On veut un minimum de 2 200 cm². La valeur de x sera bien inférieure à 20 cm.	Chaque petit carreau représente un carré de 10 cm de côté. Alors x = 200 cm. On compte 64 + 72 = 136 petits carrés dans la partie blanche, soit 13 600 cm².

Aire de la lettre H
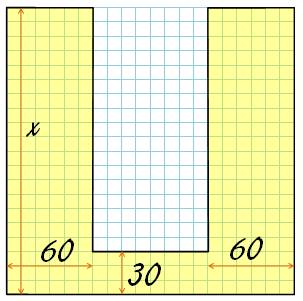
Plutôt que de prendre les deux parties ajourées du H, il est plus facile da faire descendre la barre du H vers le bas pour former un U. On calcule alors l'aire de l'unique partie blanche. La hauteur vaut : x – 30 La largeur (sachant que la lettre est dans un carré) vaut: x – 60 – 60 = x – 120 L'aire est égale à: (x – 30) (x – 120) = x² – 30x – 120x + 3 600 = x² – 150x + 3 600

Aire à ne pas dépasser
Voyons d'abord l'égalité Si l'aire valait 2200, on aurait: A(x) = x² – 150x + 3 600 = 2 200 D'où l'équation: x² – 150x + 1 400 Qui se factorise facilement (ci-contre): (x – 140) (x – 10) Passage à l'inégalité Dire que A(x) 2 200 c'est dire que: x² – 150x + 1 400 2 200 Et en remplaçant: (x – 140) (x – 10) 2 200	Deux possibilités pour factoriser 1) On nous a proposé la réponse: (x – 140) (x – 10) Alors, on développe pour vérifier = x² – 140x – 10x + 140 x 10 = x² – 150x + 1 400 La factorisation est justifiée. 2) On calcule Il faut chercher deux nombres dont le produit est 1 400 et la somme 150. Pourquoi ? Voyez comment ces nombres se sont formés dans le développement de (x – 140) (x – 10) 3) Ensuite, on se dit que l'on va tenter le plus simple: 150 et 140 sont proches, alors on teste 140 + 10 pour faire 150 et 140 x 10 = 1 400. Bingo ! On a donc: x² – 150x + 1 400 = (x – 140) (x – 10)

Voir Équation du deuxième degré – Somme et produit

Signe de (x – 140) (x – 10)

Deux points singuliers: x = 10 et x = 140

Pour x < 10, par exemple 1, alors (1 – 140) (1 – 10)
=> produit de deux nombre négatifs
=> positif

Pour x >140, par exemple 1000, alors (1000 – 140) (1000 – 10)
=> produit de deux nombre positifs
=> positif

Entre les deux, par exemple 100, alors (100 – 140) (100 – 10)
=> produit d'un nombre négatif par un positif
=> négatif

Résumé

<10	x = 10		x = 140	> 140
+	0	–	0	+

Choix de X
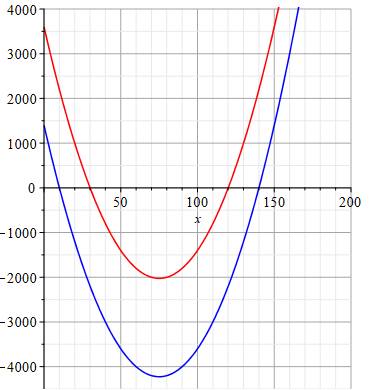
Sachant que x > 130, le tableau montre que l'on aura notre aire minimale de 2200 cm² pour x = 140 cm. Et une aire plus grande pour x > 140 cm Bonus Les courbes en bas montrent: en rouge, l'aire exacte de la partie blanche de la lettre H, en bleu, la condition pour avoir une surface minimale de 2 200 cm². Dans un cas comme dans l'autre, l'aire doit être positive donc dans la partie des y > 0. Pourquoi pas la partis positive de gauche (x < 30 ou x < 10) ? Si on reprend la formulation du calcul de l'aire, on obtient le produit de deux valeurs négatives. Or les longueurs sont des valeurs positives. Ce qui exclut ces cas pour des petits x.	Lettre H avec partie blanche = 2 200 cm² Courbes de faisabilité Rouge: A(x) = x² – 150x + 3600 Bleue: A(x) = x² – 150x + 1400

Retour	Initiation au premier degré Familiarisation avec la tangente
Suite	Fermier et pommes de terre Parcours sur un cube Polynômes Dérivées Équations du deuxième degré
Voir	Initiation au calcul Initiation aux équations Débutants / Novices
Cette page	http://villemin.gerard.free.fr/aExercic/Lycee/Lettre%20H.htm