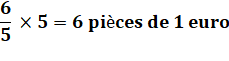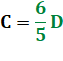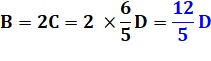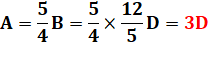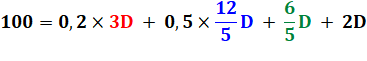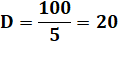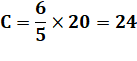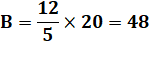|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Les 100 euros en pièces de monnaies Problème facile lorsqu'on
connait les équations. Mais sinon, comment s'y
prendre? Un raisonnement ou un graphique. |
|
|
|||
|
Problème Lilou possède la somme de
100 euros en pièces de 20 centimes, 50 centimes, d'1euro et de 2 euros. Elle promet la moitié de sa
fortune à son petit frère s'il parvient à lui donner le nombre de chaque type
de pièce. Elle lui indique:
Aidez le petit frère de
Lilou à répondre au défi de sa sœur. |
Je visualise la situation
|
||
|
Solution pas à pas |
|
||
|
Pièce de 2 euros |
S'il n'y
avait que des pièces de 2 euros, il y en aurait: 100 / 2 = 50. C'est la
valeur maximum de la quantité de pièces de 2 euros. Je ne
sais pas encore combien il y en aura, alors je note ce nombre inconnu par la
lettre D, pour le moment. |
||
|
Pièces de 1 euro = les six cinquièmes du nombre des pièces de 2 euros |
Je note
que la quantité de pièces de 1 euro est un peu plus grande (5/6 = 1,2) que
celle de deux euros. Cette
proportion veut dire que chaque fois que j'ai une pièce de 2 euros, elle est
accompagnée de 6/5 pièce de 1 euro, soit 1,2 euro. Oups!
J'ai des morceaux de pièces de 1 euro. Pas possible! Alors, pour tomber
juste, il faut 5 fois plus de pièces de 2 euros. Et, avec 5 pièces de 2
euros, j'ai:
Ce qui
fait une somme-paquet total de 5 x 2 + 6 x 1 = 16 euros. |
||
|
Bilan pour 1 euro et 2 euros |
Pour
satisfaire la fraction 5/6, j'ai été amené à dire que les pièces de 5 euros
allaient par groupes de 5 et celles de 1 euro par groupe de 6, ce qui forme
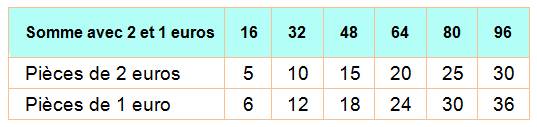
des paquets de 16 euros. En
prenant plus ou moins de ces paquets de 16 euros, je dois m'approcher de 100
euros et compléter avec les pièces de 50 et
20 centimes. On peut
donc avoir ces paquets de 16 euros:
|
||
|
Pièces de 50 centimes: il y
en a deux fois plus que celles de 1 euro |
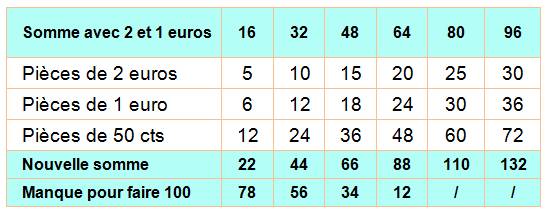
Ajoutons
les pièces de 50 cts en bonne proportion dans notre tableau et voyons le
nouveau total.
Nous en
avons profité pour indiquer le montant nécessaire pour arriver à faire une
somme égale à 100 euros. |
||
|
Pièces de 20 cts = cinq quarts des pièces de 50 centimes |
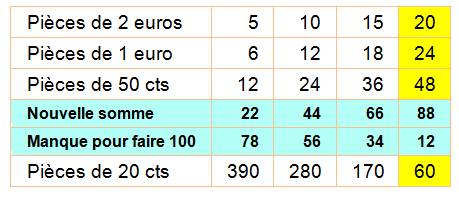
Facile de
compléter le tableau avec la quantité de pièces de 20 centimes pour combler
le manque. Par exemple: il en faut 78 x 5 = 390 pour la première colonne.
Reste à
trouver quelle est la colonne qui donne les 5/4. Il s'agit
de la dernière avec 60 / 48 = 5 /4. La
dernière colonne est donc la solution. |
||
|
|
||
|
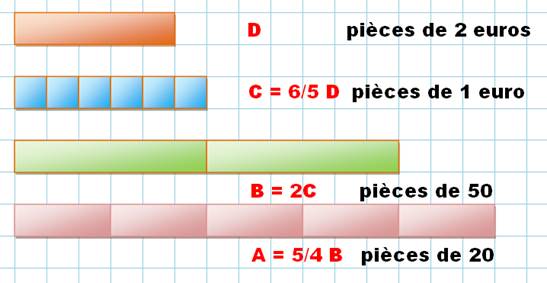
Un graphique va nous
permettre de visualiser les proportions et d'apprécier les relations entre
les fractions. |
||
|
Quantité de pièces d'un euro vaut les six
cinquièmes du nombre des pièces de 2 euros Quantité de pièces de 50 centimes vaut le double
de celui des pièces d'un euro. Autant de pièces de 20 centimes que les cinq
quarts des pièces de 50 centimes, |
Graphiques illustrant les proportions
Note: pour
pouvoir représenter la fraction 6/5, j'ai dû prendre D = 5. |
|
|
Raisonnement |
Chaque
fois que j'ai D pièces de 2 euros, automatiquement, j'ai toutes ces
proportions pour les autres pièces. Ces pièces dans ces proportions forment
un paquet qui vaut une certaine somme S. Ce qui
veut dire que la somme de 100 euros est constituée d'un certain nombre de
fois ce paquet, cette somme S. |
|
|
Somme S minimale |
Pour obtenir
un nombre entier de pièces de 1 euro, il faut un minimum de 5 pièces de 2
euros. Si D = 5 alors C = 6, B = 12 et A = 15. La somme
minimale est égale à: S = 5 x 2 + 6 x 1 + 12 x 0,50 + 15 x 0,20
= 10 + 6 + 6 + 3 = 25 euros |
|
|
Combien de S pour atteindre 100? |
Avec
quatre fois cette somme, on obtient 4 x 25 = 100 euros. Traduit
en pièces: D = 20, C = 12, B = 48 et A = 60. |
|
|
|
||
|
On écrit simplement les
relations entre les quatre valeurs inconnues A, B, C et D |
||
|
Somme |
|
|
|
Proportions |
|
|
|
Proportions dans somme |
|
|
|
Quantité de pièces |
|
|
![]()
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()