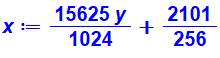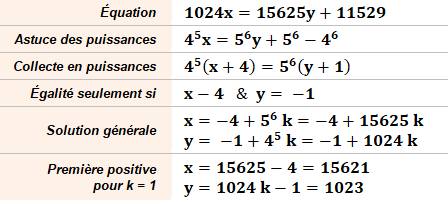|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SINGE & NOIX de COCO
Historique Il existe plusieurs versions de ce défi
mathématique. Vers 850, le mathématicien indien Mahavira
propose cette énigme parmi d'autres défis de partage. En 1888, Lewis Carroll pose un problème
semblable. En 1926, le romancier américain Ben Ames Williams
publie cette énigme sous le nom de Coconuts, sans donner la réponse. En 1958, Martin Gardner publie ce défi dans
Scientific American et comme premier article dans son livre: Colossal book of mathematics
Aujourd'hui, il existe de nombreuses variantes et
généralisations. |
Anglais: The monkey and the coconuts
|
|
|
|
Énigme: version de
Williams Cinq hommes et un
singe font une provision de noix de coco. Durant la nuit le
premier se lève et prend un cinquième des noix de coco; il en reste une qu'il
donne au singe. Le deuxième se lève
un peu plus tard et fait la même chose: il prend un cinquième de qui reste et
en donne une au singe. Même chose jusqu'au
cinquième. La troupe se lève
au petit matin comme si de rien n'était; chacun se sent coupable et ne dit
rien. Ils décident de faire le partage à parts égales. Chacun reçoit sa
part et il ne reste pas de noix de coco
(version de Williams; la version originale laisse une
noix de coco à la fin). Combien de noix de
coco au départ ? Réponse Il
y en a une infinité de solutions, la plus petite est 3 121
noix de coco au départ. La
version originale conduit à 15 621
noix de coco au départ. |
|
|
|
|
|
L'illustration
montre la solution numérique la plus petite
et la mise en équation. L'inconnue
y est la quantité partagée à la
fin et reçue par chacun. En
descendant sur le schéma, on trouve la situation pour le cinquième homme (5y) puis les suivants pour arriver à
la quantité de départ x. En
remontant, on visualise la part qui reste (trapèze jaune) et la part prélevée
par l'homme et la noix destinée au singe. Les lettres A, B, C, D et E
représentent la quantité totale de noix
dont dispose chaque homme avant prélèvement. Par exemple, le premier homme
dispose de A = 3121 noix. Par rapport au tas B = 5 x 499 + 1 = 2496 dont
dispose le deuxième homme, la part prélevée vaut le quart: 2596 / 4 = 624. Le
tas du premier homme est ainsi: 5 x 624 + 1 = 3121. Solution
numérique
Équations
Note: chacun aura la part commune 204 plus la part
mise de côté. Par
exemple, le premier aura: 204 + 624 = 828 noix de coco. En
remplaçant de proche en proche et en
simplifiant (en bleu), on obtient, l'équation diophantienne suivante:
En
supprimant le dénominateur (multiplication par 1024): 1
024 x – 15 625 y = 8 404 210 x –
56 y = 8 404 |
|
|
|
|
|
La
résolution
exige que: Si g = PGCD (1 024,
15 625), alors 8 404 = k·g En l'occurrence g = 1 (l'un est puissance
de 2 et l'autre est puissance de 5). Il
faut se débrouiller (heuristique) pout trouver une solution par essais
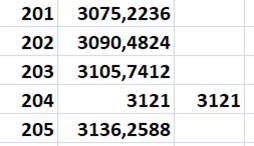
successifs avec tableur par exemple: Première colonne y, deuxième x et
troisième colonne détection d'un entier avec test x = tronque(x).
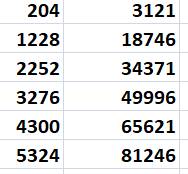
Ayant
une solution (3 121 et 204), nous pouvons en donner une infinité x
= 3 121 + 15 625 k y
= 204 + 1 024 k Les
valeurs suivantes:
|
|
|
|
||
|
Il est possible d'atteindre les solutions par le
calcul. Il s'agit de résoudre une équation diophantienne
de type: ax+ by = c. On procède en deux
temps: 1)
Application de l'algorithme
d'Euclide pour la recherche de PGCD. 2)
Puis, avec ces données, rebroussement du calcul (lignes avec =>) Ce procédé produit une solution de référence x et
y. Injectée dans la solution
générale en k, on a accès à une infinité de solutions. On cherche celle qui donne la plus petite valeur
positive. Une simple division permet d'avoir l'ordre de grandeur. Nous avons ainsi accès la solution minimale (x0,
y0) par calcul et non par essais successifs. |
|
|
|
|
||
|
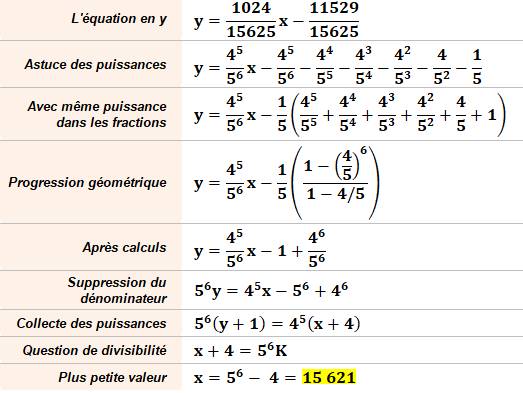
Bien sûr, la résolution par algorithme d'Euclide est toujours possible. Ici, c'est cette propriété qui est exploitée: |
Dans le cas où il reste
une noix de coco en final, la solution minimale est x = 15 621 et y =
1 023. En reprenant, les calculs précédents, l'équation
devient:
45
x = 56 y + 56 – 46
|
|
|
Pour information, une variante plus recherchée met en évidence progression
géométrique. |
|
|
|
Five sailors are shipwrecked
on a desert island. They quickly determine that the only other inhabitant of the
island is a monkey and that the only food is coconuts. They set about
collecting as many coconuts as they can and put them all in a very large
pile. By nightfall they are too tired to divide the harvest; so they agree to
go to sleep and share the coconuts equally the next morning. During the night one sailor
awakens, suspicious that the others might try to cheat him, and decides to
take his portion then and there and not wait until morning. He divides the
coconuts into five piles and finds there is one coconut left over, which he
gives to the monkey. He hides one of the five piles, then puts the rest of
the coconuts back into a pile and returns to sleep. Later a second sailor
awakens with the same suspicions and does the same thing: He divides the coconuts
into five piles, leaving one extra, which he gives to the monkey. Then he
hides what he thinks is his share, puts the remaining coconuts into a pile
and goes back to sleep. One after the other, the
rest of the sailors do the same. They each take one fifth of the coconuts in
the pile (there is always an extra one, which is given to the monkey) and
then return to sleep. When the sailors awaken the
next morning they all notice the coconut pile is much smaller than it was the
night before, but since each man is as guilty as the others, no one says
anything. They divide the coconuts (for the sixth time) and again there is
one left for the monkey. How many coconuts were in
the original pile? |
Cinq marins font naufrage
sur une île déserte. Ils réalisent rapidement que le seul autre habitant de
l'île est un singe et que la seule nourriture est la noix de coco. Ils
entreprennent de ramasser le plus de noix de coco possible et faisant un très
gros tas. À la tombée de la nuit, ils sont trop fatigués pour partager la
récolte; ils conviennent donc d'aller dormir et de partager les noix de coco
de manière égale le lendemain matin. Pendant la nuit, un marin se
réveille, soupçonnant que les autres pourraient essayer de le tromper, et
décide de prendre sa part sur-le-champ sans attendre le matin. Il divise les
noix de coco en cinq tas et constate qu'il en reste une, qu'il donne au
singe. Il cache l'un des cinq tas, puis remet le reste des noix de coco en
tas et retourne se coucher. Plus tard, un deuxième marin
se réveille avec les mêmes soupçons et fait la même chose : il divise les
noix de coco en cinq tas, en donne une noix en trop au singe. Puis il cache
ce qu'il pense être sa part, met les noix de coco restantes dans un tas et se
rendort. L'un après l'autre, les
autres marins font de même. Ils prennent chacun un cinquième des noix de coco
du tas (il en reste toujours une, qu'ils donnent au singe), puis se
rendorment. Lorsque les marins se
réveillent le lendemain matin, ils remarquent tous que le tas de noix de coco
est beaucoup plus petit que la veille, mais comme chaque homme est aussi
coupable que les autres, personne ne dit rien. Ils divisent les noix de coco
(pour la sixième fois) et il en reste une pour le singe. Combien de noix de coco y
avait-il dans la pile initiale? |
![]()
|
Voir |
|
|
Aussi |
|
|
|
|
|
Cette page |
![]()