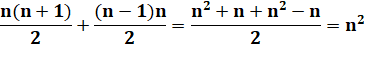|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Énigme du partage en 1/17 Un père partage son héritage
en accordant une part fixe et une part variable en fraction égale à 1/17. Belle énigme qui semble difficile à résoudre.
Voyons cela. Généralisation à n'importe
quelle fraction en 1/k. |
|
|
||
|
Le
testament stipule que le premier fils recevra une part fixe F, le deuxième,
deux parts fixes (2F), et ainsi de suite; chacun une part fixe multipliée par
son rang de filiation. De plus chacun
recevra 1/17 de ce qui reste avant de passer au frère de rang suivant. Ainsi,
l'héritage est totalement partagé et, de plus, chacun recevra exactement la
même part. Combien
de fils se partagent l'héritage ? |
Un raisonnement direct consiste à calculer la part de chacun en
commençant par le premier fils: P1 = F + 1/17 (T – F) La part du premier est égale à la part fixe plus 1/17e de
ce qui reste; soit le total (T) moins ce qui a été distribué (F). Le deuxième reçoit: P2 = 2F + 1/17 (T – P1 –
2F) Etc. Calcul laborieux! |
|
|
Le bon
raisonnement consiste à partir du dernier fils, le n° X. Le partage étant
complet, le dernier reçoit sa part fixe (X fois F) et 1/17e de
rien. |
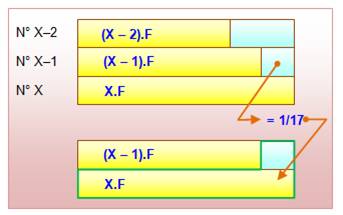
Le dernier reçoit PX = X.F + 1/17 (0) = X.F |
|
|
L'avant-dernier
reçoit (x – 1) fois F et 1/17e du reste que nous pouvons évaluer. Le reste (zone entourée de vert) vaut 2 fois le
montant de chacun (X.F) moins le montant reçu par l'avant dernier (X – 1) F. |
Reste (en vert) = 2X.F – (X – 1)F
PX-1 = (X – 1)F + 1/17 (2X.F – (X – 1)F) |
|
|
Les deux
derniers reçoivent la même somme. Notons la
simplification par F qui indique que le problème ne dépend pas de la valeur
du don fixe F. La
résolution est simple. |
X.F = (X – 1)F + 1/17 (2X.F – (X – 1)F) X = (X – 1) + 1/17 (2X – (X – 1)) 0 = – 1 + 1/17 (X – 1) X – 1 = 17 X = 16 |
|
|
|
||
|
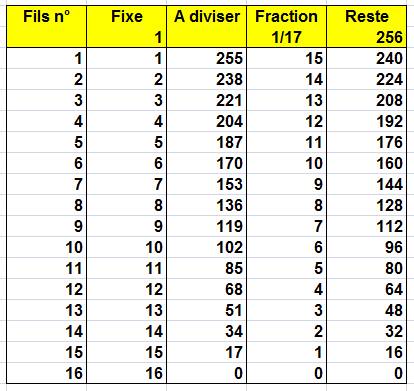
Le fils
n°1 reçoit une part fixe de F = 1 euro
(on sait qu'on aurait pu prendre n'importe quelle valeur). En
partant d'un total T = 256 euros (valeur
ajustable une fois le tableau terminé), il reste 256 – 1 = 255 euros à
partager. Le premier fils en reçoit 1/17e, soit 15 euros. Le fils
n'°1 reçoit donc la somme de 1 + 15 = 16 euros. Le fils
n°2 reçoit la part fixe de 2F = 2 euros et la part variable de 1/17 (240 – 2)
= 1/17 (238) = 14. Soit une somme de 2 + 14 = 16 euros. Etc. |
La valeur de tête, ici à 256, est ajustée par approximations
successives pour obtenir 0 en bas du tableau. |
|
|
Ces
valeurs tabulées montrent explicitement le montage de cette énigme. Le total des sommes fixes est la somme des nombres de 1 à 16 (= 17 – 1). Tandis
que celle des sommes variables est égale à la somme des nombres de 1 à 15 fois 17, puis divisée par 17. |
Total = (1 + 2 + … + 16) + (15 + 14 + … + 0) = ½ (16 x 17) + ½ (15x
16) = 136 + 120 = 256 Le total vaut aussi 16 fois (16
fils) la somme 16 (part de chacun) = 16² = 256 On retrouve bien le carré avec la somme des nombres:
|
|
Voir Tableur
Bilan
|
Avec
cette sorte de partage en 1/k,
|
|
|
||
|
Héritage:
le fils n°k reçoit k plus 1/3 de ce qui reste. Combien de fils? Solution Nous reprenons exactement le même principe
que celui exposé au paragraphe précédent. La
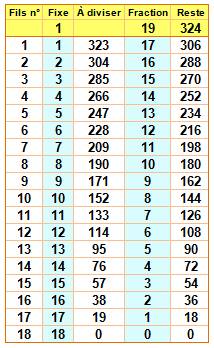
solution est générale quelle que soit la fraction. Cas de la fraction 1/19 avec 18² =
324
|
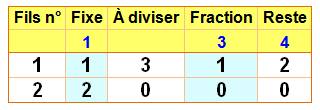
Avec 1/17 nous avions 16 fils (17 – 1); avec 1/3, il y a 2 fils. L'héritage se monte à: ½ (2 x 3 ) +
½ (1 x 2) = 4 ou plus simplement à 2² = 4 Tableau récapitulatif avec la
faction 1/3
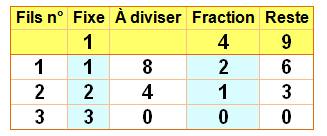
Tableau récapitulatif avec la
faction 1/4 avec 3² = 9
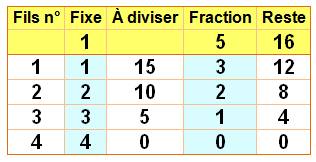
Tableau récapitulatif avec la
faction 1/5 avec 4² = 16
|
|
Voir Carrés
|
|
||
|
Revenons
aux deux équations établies au début pour le premier et le deuxième fils. Il est
possible de les résoudre et trouver la solution. |
P1 = F + 1/17 (T – F) P2 = 2F + 1/17 (T – P1 – 2F) |
|
|
Qui
s'écrivent sans dénominateur et en prenant F = 1 |
17P1 = 17 + T – 1 17P2 = 34 + T – P1 – 2 |
|
|
Or, les
parts sont égales: P1 = P2 Puis sans
le dénominateur. |
17 + T – 1 = 34 + T –1/17(17 + T – 1) – 2 17² + 17T – 17 = 2x17² + 17T – 17 – T + 1 – 34 |
|
|
Simplification: |
0 = 17² – T – 33 |
|
|
Finalement: |
T = 256 |
|
Voir Système
d'équations
![]()
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()