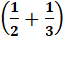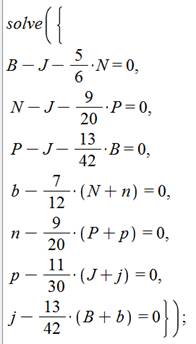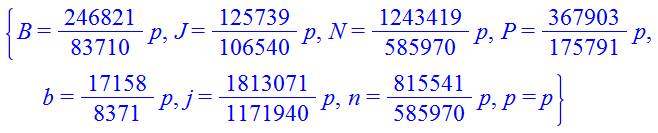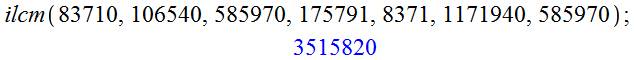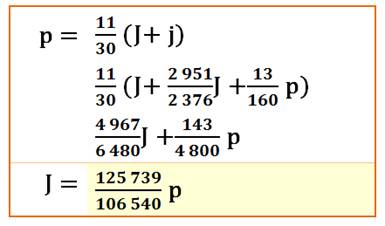|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Problème des bœufs d'Hélios Les bœufs d'Archimède / Les
taureaux d'Archimède Le troupeau du soleil / Le troupeau
d'Hélios Problème qu'Archimède ( Il s'agit
de retrouver la quantité de bœufs à partir de sept conditions formant équations. Cette première partie n'est pas très dure à
résoudre même si la solution donne de grands nombres. Deux
conditions complémentaires (apocryphe?)
rendent le problème quasi-impossible. Découvert en 1773 par
Gotthold Lessing dans une bibliothèque de Wolfenbüttel (Allemagne). Résolu en
1880 par A. Amthor. |
Anglais: The cattle problem,
Helios cattle, Archimedes' cattle problem, oxen of the sun
Archimedes'
Problema Bovinum
|
|
|
|
Si tu
es diligent et sage, ô étranger, calcule le nombre de têtes de bétail du
troupeau du soleil qui autrefois paissait dans les champs de l'île de
Thrinacian …. Le
dieu soleil (Hélios) possède un
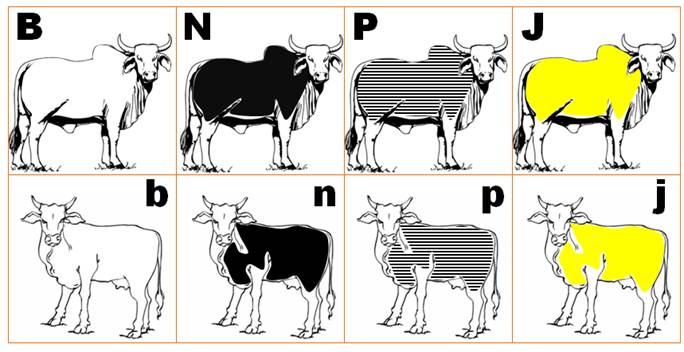
troupeau de taureaux et de vaches, dont une partie était blanche, une partie noire,
une partie pie, et la quatrième jaune. Version anglaise:
The sun god had a herd of cattle consisting of bulls and cows, one part of which was white, a second black,
a third spotted, and a fourth brown. Robe pie: qui est composée d'une couleur en plus du blanc; l'anglais dit
tacheté (spotted).
Pour
les taureaux:
Pour
les vaches:
|
|
Bœufs d'Hélios (Odyssée d'Homère)
|
Ulysse
vient de passer les écueils de Charybde et Scylla (détroit de Messine entre
Italie et Sicile). Circé
(enchanteresse, fille d'Hélios) et le devin Tirésias le mettent en garde: sur
l'île de Thrinacia (Sicile ou Malte?), ne pas toucher au troupeau sacré
d'Hélios, le dieu du soleil.
L'Odyssée d'Homère -
Traduction de Leconte de Lisle (1818-1894) Rappel:
femme d'Ulysse: Pénélope
et leur fils Télémaque Les
compagnons d'Ulysse sont à bout de
force et imposent un arrêt sur l'île pour se reposer. Le vent se lève qui
oblige l'équipage à reste sur l'île. Les provisions venant à manquer, ils
succombèrent et mangèrent les plus belles bêtes d'Hélios. Celui-ci
réclame vengeance auprès de Zeus, lequel foudroie le navire d'Ulysse,
l'épargnant seul, car il n'a pas mangé de cette viande. |
Voir Factorisation de Pénélope
|
|
||
|
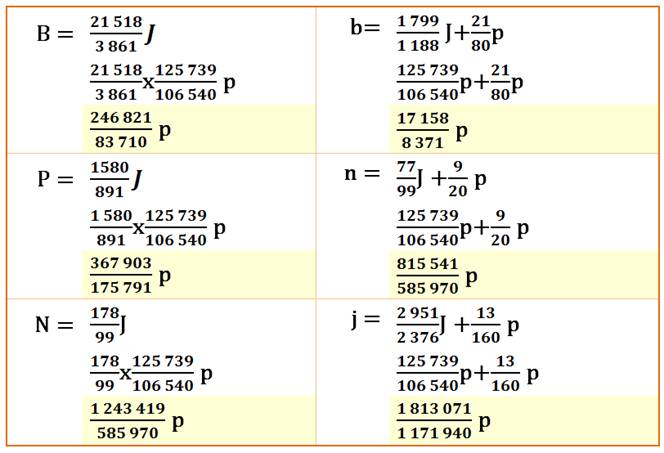
Formulations de la première proposition
Formulation symbolique B = J + |
|
|
|
|
||
|
|
|
|
Alors, la solution ne sera
connue qu'à une constante de proportionnalité près (k, un entier).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
B + N =
c² P + J = ½
t (t + 1) avec c et t deux entiers |
|
|
|
B + N = 17
826 996 k = c² = 22 x 3 x 11 x 29 x 4659 k = 22 x 4 456 749 k k = 4 456 749 h² |
|
|
|
P + J = ½
t (t + 1) = 11 507
447 x 4 456 749 h² = 512 85
802 909 803 h2 8/2 t (t
+ 1 ) + 1 = 4t² + 4t + 1 = (2t +
1)2 (2t + 1)2 = 8 x 512 85 802 909 803 h2 + 1 = 410 286
423 278 424 h² + 1 = 23
x 3 x 7 x 11 x 29 x 353 x 4 6572 h² + 1 = 4 729 494 x 9 314² h² + 1 u² = 4 729 494 v² + 1 v² = 9 314² h² |
|
|
|
u² – k . v² = 1
v avec k = 4 729 494 = 2 x 3 x 7 x 11 x
29 x 353 |
|
|
|
En 1965, la valeur de
la taille du troupeau fut calculée par ordinateur en pratiquement huit heures
de calcul – Williams et al. Taille du troupeau
Il faut 52 pages pour imprimer ce nombre. |
|
Conclusion
|
Il
est plus que probable qu'Archimède n'a pas résolu ce problème. On se demande même
si, taquin, il ne voulait pas mettre en difficulté ses collègues. Plus
tard, en arrivant sur l'extravagante équation de Pell,
certains mathématiciens ont voulu interpréter les contraintes. Un exemple: le
carré appliqué au troupeau voudrait dire que les bêtes sont mises dans une
grille carrée; or le bovin étant plus long que haut, on aboutirait à un
rectangle et la contrainte deviendrait: T
= n . m et non T = c². |
![]()
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()