|
|||||||||||||||||||||||
![]()
|
RÉDUITES ou Fractions d'approximation des
constantes Tout nombre irrationnel peut être exprimé par
une fraction continue. En ne
retenant que les n premiers termes, la fraction obtenue est une bonne
approximation du nombre. La fraction correspondant à ce développement partiel
de la fraction continue est dite "réduite"
de n. |
Efficacité
|
La
réduite est une fraction
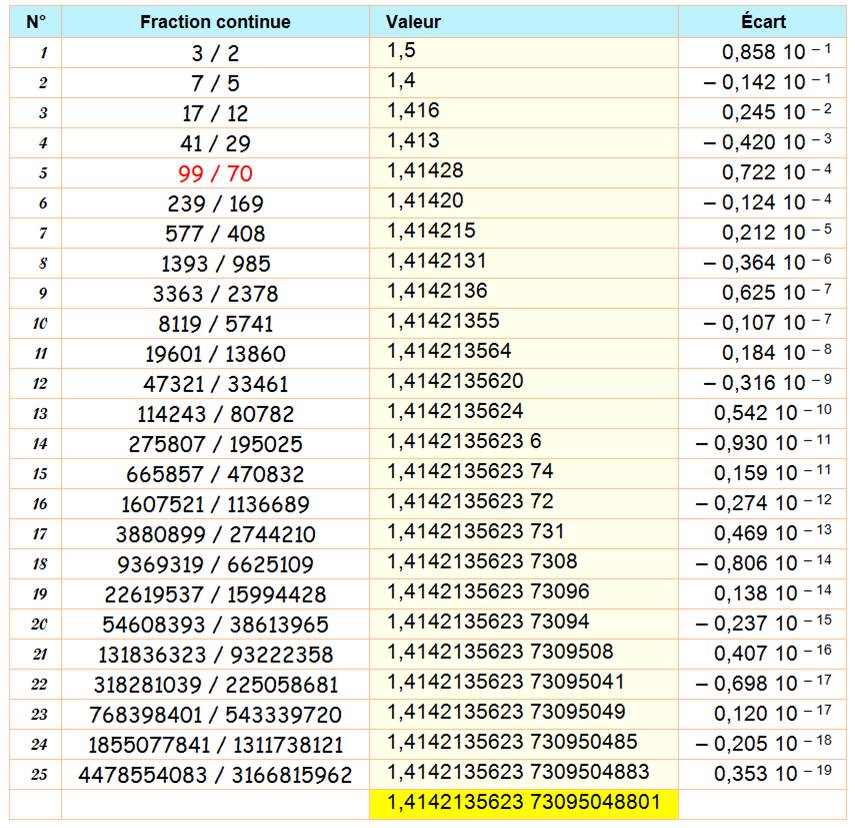
"efficace". Par exemple, pour racine de 2 avec trois chiffres, on obtient:
239 / 169 = 1, 4142… soit cinq chiffres significatifs alors que la fraction
évidente à trois chiffres: 141 / 100 ne donne que trois chiffres
significatifs. On montre que les réduites obtenues avec la fraction continue
sont les plus "efficaces" (ou optimales). Elles encadrent au mieux la valeur du nombre
représenté. Il n'y a pas de fractions plus optimales
avec la même quantité de chiffres. |
Voir Calcul avec le théorème de Dirichlet /
Nombres
de Lagrange
|
|
|
|
Fraction continue:
[1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, ...]
|
|
Voir Racine de 2
|
|
|
|
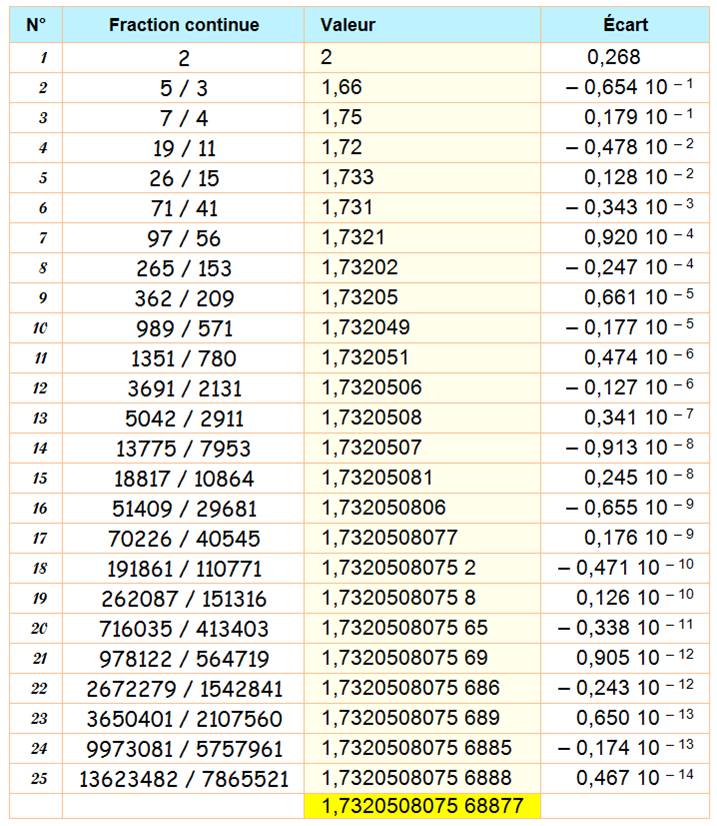
Fraction continue:
[1, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2,
1, ...]
|
|
Voir Racine de 3
|
|
|
|
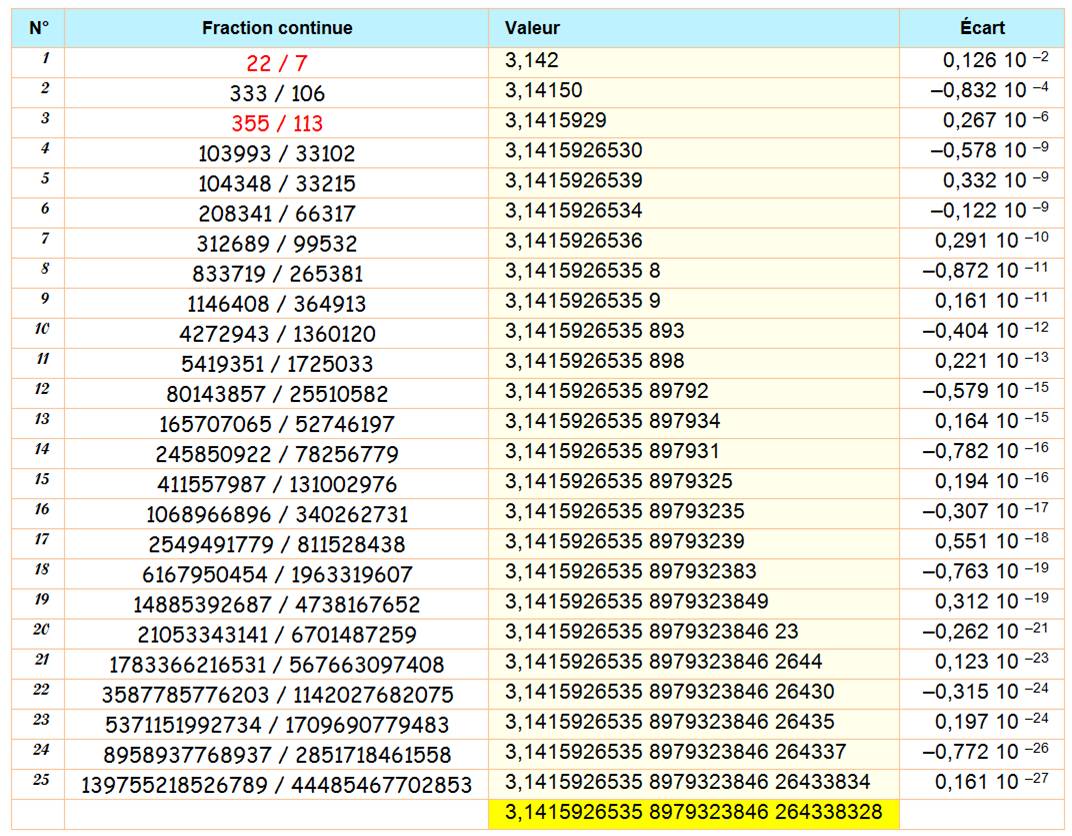
Fraction continue:
[3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1,
1, 15, ...]
|
|
Voir Constante Pi
Curiosités avec Pi

|
|
|
|
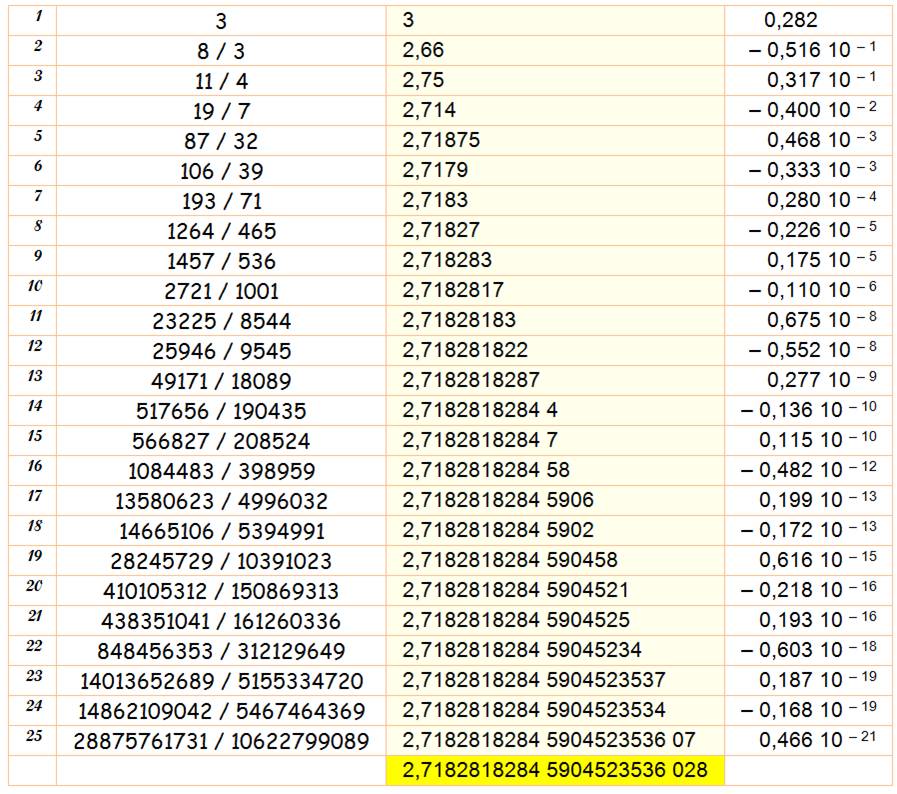
Fraction continue: [2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1,
10, 1, 1, 12, 1, 1, 14, 1, 1, 16, 1, 1, ...]
|
|
|
|
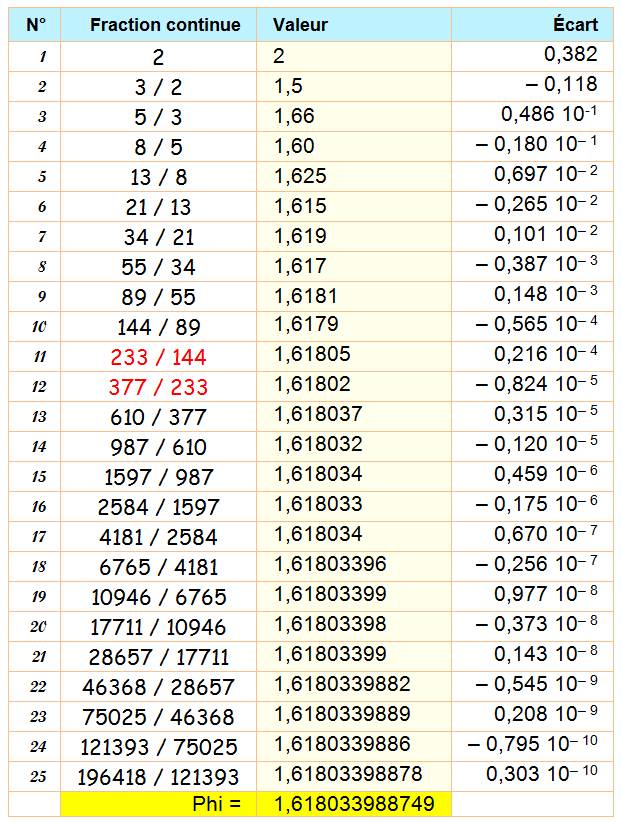
|
|
Fraction continue: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, ...]
|
|
Voir Nombre d'or/ Autres fractions continues avec
Phi
Programmation Maple
|
Exemple: calculer les cinq plus petites réduite de
racine de 17:
|
|
Fractions continues et réduites des nombres
premiers de 2 à 113 2, [1, 2, 2, 2, 2], [1, 3/2, 7/5, 17/12, 41/29] 3, [1, 1, 2, 1, 2], [1, 2, 5/3, 7/4, 19/11] 5, [2, 4, 4, 4, 4], [2, 9/4, 38/17, 161/72, 682/305] 7, [2, 1, 1, 1, 4], [2, 3, 5/2, 8/3, 37/14] 11, [3, 3, 6, 3, 6], [3, 10/3, 63/19, 199/60, 1257/379] 13, [3, 1, 1, 1, 1], [3, 4, 7/2, 11/3, 18/5] 17, [4, 8, 8, 8, 8], [4, 33/8, 268/65, 2177/528, 17684/4289] 19, [4, 2, 1, 3, 1], [4, 9/2, 13/3, 48/11, 61/14] 23, [4, 1, 3, 1, 8], [4, 5, 19/4, 24/5, 211/44] 29, [5, 2, 1, 1, 2], [5, 11/2, 16/3, 27/5, 70/13] 31, [5, 1, 1, 3, 5], [5, 6, 11/2, 39/7, 206/37] 37, [6, 12, 12, 12, 12], [6, 73/12, 882/145, 10657/1752, 128766/21169] 41, [6, 2, 2, 12, 2], [6, 13/2, 32/5, 397/62, 826/129] 43, [6, 1, 1, 3, 1], [6, 7, 13/2, 46/7, 59/9] 47, [6, 1, 5, 1, 12], [6, 7, 41/6, 48/7, 617/90] 53, [7, 3, 1, 1, 3], [7, 22/3, 29/4, 51/7, 182/25] 59, [7, 1, 2, 7, 2], [7, 8, 23/3, 169/22, 361/47] 61, [7, 1, 4, 3, 1], [7, 8, 39/5, 125/16, 164/21] 67, [8, 5, 2, 1, 1], [8, 41/5, 90/11, 131/16, 221/27] 71, [8, 2, 2, 1, 7], [8, 17/2, 42/5, 59/7, 455/54] 73, [8, 1, 1, 5, 5], [8, 9, 17/2, 94/11, 487/57] 79, [8, 1, 7, 1, 16], [8, 9, 71/8, 80/9, 1351/152] 83, [9, 9, 18, 9, 18], [9, 82/9, 1485/163, 13447/1476, 243531/26731] 89, [9, 2, 3, 3, 2], [9, 19/2, 66/7, 217/23, 500/53] 97, [9, 1, 5, 1, 1], [9, 10, 59/6, 69/7, 128/13] 101, [10, 20, 20, 20, 20], [10,
201/20, 4030/401, 80801/8040, 1620050/161201] 103, [10, 6, 1, 2, 1], [10, 61/6, 71/7, 203/20, 274/27] 107, [10, 2, 1, 9, 1], [10, 21/2, 31/3, 300/29, 331/32] 109, [10, 2, 3, 1, 2], [10, 21/2, 73/7, 94/9, 261/25] 113, [10, 1, 1, 1, 2], [10, 11, 21/2, 32/3, 85/8 |
Voir Programmation – Index
![]()
|
Voir |
|
|
Cette page |
![]()