|
|||||||||||||||||||||||||||
![]()
|
ORDRE de GRANDEUR Comparaison des nombres en
puissance de 10
|
|
|
||
|
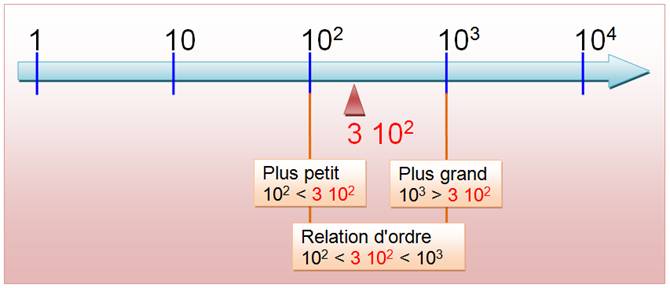
Arrondi: 300 est plus proche
de 100 (écart 300) que de 1000 (écart 700). |
n = 3 102 n est plus petit que 1000 = 103 n est plus grand que 100 = 102
102 < 3 102 < 103 3 102 |
|
|
A est un nombre compris
entre 1 et 5 (non compris)
B est un nombre compris
entre 5 (compris) et 2 (non compris)
|
n = A x 10k
n m = B x 10k
m |
|
Illustration
|
Il
faut procéder avec méthode: 1) positionner
le nombre sur la droite
des réels; 2) noter
l'inégalité avec le plus petit; 3) noter
l'inégalité avec le plus grand; 4) écrire
la double inégalité en respectant les sens des inégalités; et 5) donner
l'arrondi en appréciant l'écart avec le plus grand et le plus petit, sachant
que si le nombre est au milieu, l'arrondi sera égal au plus grand. |
|
Exemples divers |
n = 2,2 x 1010
n n = 7,525 x 1010
n |
|
Exemples particuliers |
n = 1,000 001 1010
n n = 5 x 1010
n n = 9,999 999 x 1010
n |
|
|
||
|
|
n = 0,2 x 1010 n = (0,2 x 10) x (1010 / 10) n = 2 x 10 9
n
n = (225 / 100) x (1010 x 100) n = 2,25
x 10 11
n |
|
|
|
||
|
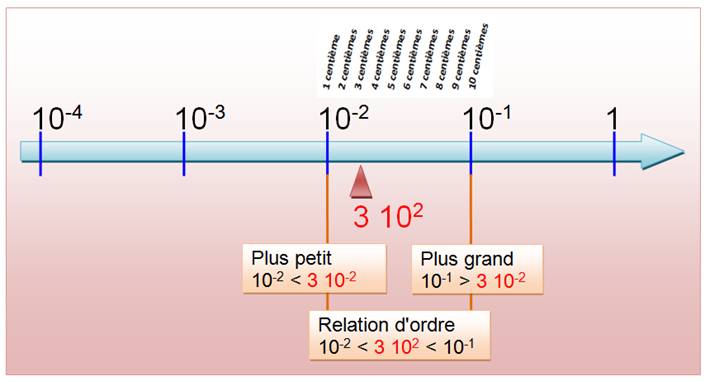
Arrondi: 3/300 est plus proche
de 1/100 (écart 2/100) que de 1/10 = 10/100 (écart 7/100). |
n = 3 10-2 n est plus petit que 1/10 = 10-1 n est plus grand
que 1/100 = 10-2
10-2 < 3 102 < 10-1 3 10-2 |
|
|
A est un nombre compris
entre 1 et 5 (non compris)
B est un nombre compris
entre 5 (compris) et 2 (non compris)
|
n = A x 10-k
n m = B x 10-k
m |
|
Bilan
|
La
même méthode s'applique. Elle a tout son intérêt ici,
car il vaut mieux repasser par toutes ces étapes pour ne pas risquer de se
tromper. |
|
Exemples divers |
n = 2,2 x 10-10
n n = 7,525 x 10-10
n |
|
Exemples particuliers |
n = 1,000 001 10-10
n n = 5 x 10-10
n n = 9,999 999 x 10-10
n |
|
Puissances de 10 cachées |
n = 0,22 x 10-10 n = (0,22 x 10) x (10-10
/ 10) n = 2,2 10-11
n |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/FORMATIO/Grandeur.htm |
![]()
