|
||||||||||||||||||||||||||||
![]()
|
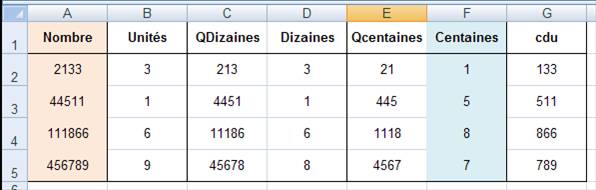
CHIFFRE des DIZAINES
|
|
Extraction des centaines
sur tableur |
|
|
|
|
|
|
||
|
|
> restart: for
N from 1000 to 2000 by 177 do QDiz:= iquo(N,10): Diz:= irem(QDiz,10): QCent:= iquo(QDiz,10): Cent:= irem(QCent,10): lprint
(N,Cent): od: 1000, 0 1177, 1 1354, 3 1531, 5 1708, 7 1885, 8 |
|
Voir Programmation
de la division et ses applications
|
|
|||
|
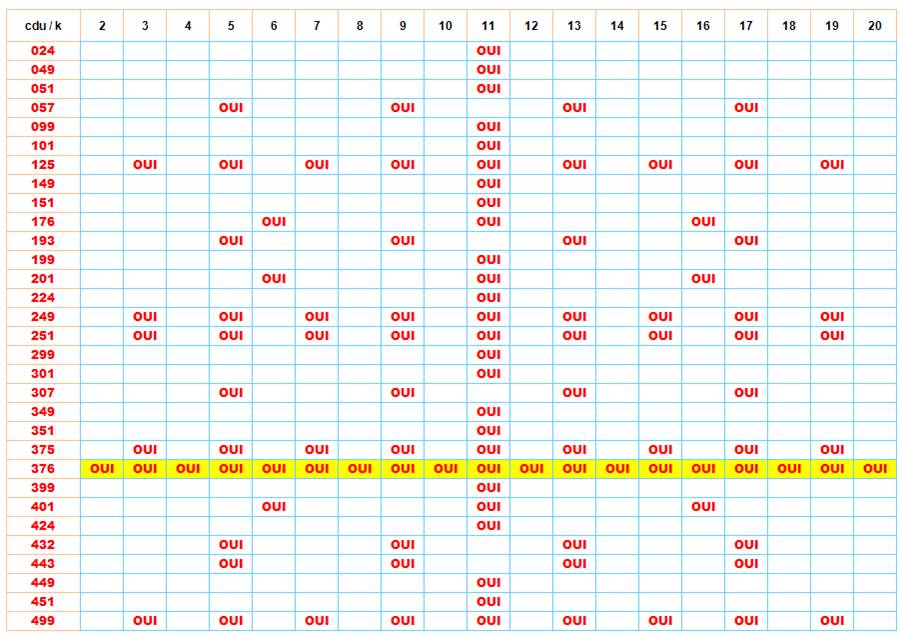
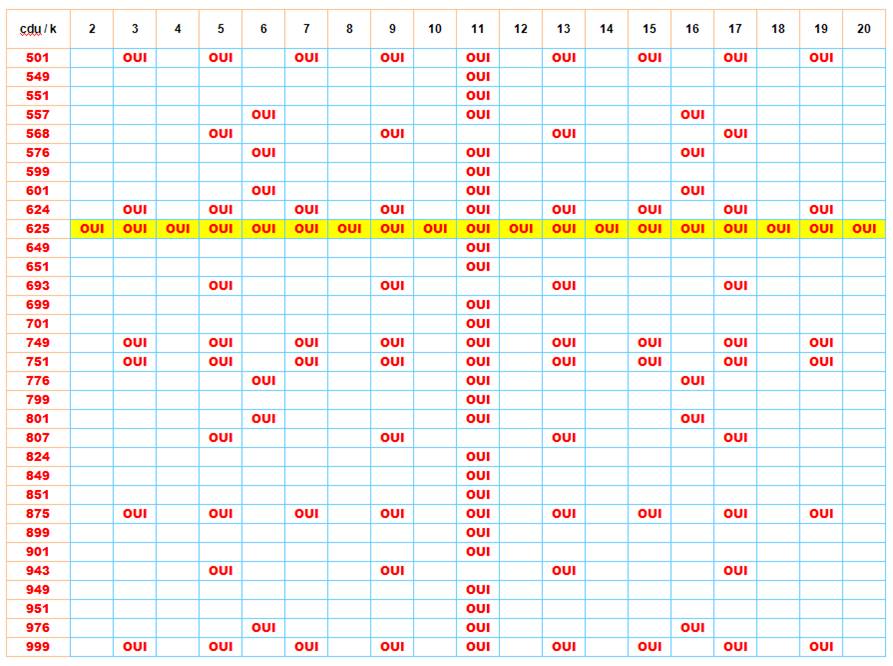
Note: les
caractères liés à "du" sont donnés sur la page dizaines et rappelés ici (blanc); les nouveaux
caractères sont en jaune. |
|||
|
2 |
u = {0, 2, 4, 6, 8} |
1234 => 4 => 1234 divisible par 2 |
|
|
4 |
2d + u divisible par 4 |
556 => 2x5+6= 16 => 556 divisible par 4 |
|
|
5 |
u = {0,5} |
12345 => 5 => 12345 divisible par 5 |
|
|
8 |
4c + 2d + u divisible par 8 |
9872 => 4x8 + 2x7 + 2 = 48 |
|
|
10 |
u = 0 |
3210 => 0 => 3210 divisible par 10 |
|
|
20 |
ud ={00, 20, 40, 60, 80} |
1220 => 20 => divisible par 20 |
|
|
25 |
du = {00, 25, 50, 75} |
1 075 => 75 => 1075 divisible par 25 |
|
|
40 |
2c + d divisible par 4 et u = 0 |
49 360 => 3x2 + 6 = 12 => 12 = 4x3; |
|
|
50 |
du = {00, 50} |
1 050 => 50 => 1050 divisible par 50 |
|
|
100 |
d = 0 et u = 0 |
45 600 => 00 => 45600 divisible par 100 |
|
|
125 |
cdu = {000, 125, 250, 375, 500, 625, 750, 875} |
7 375 => 375 => 7375 divisible par 125 |
|
|
200 |
c pair, d = 0 et u = 0 |
11 800 => 800 => 11 800 divisible par 200 |
|
|
250 |
cdu = {000, 250, 500, 750} |
45 750 => 750 => 45 750 divisible par 250 |
|
|
500 |
cdu = {000, 500} |
45 500 => 500 => 45 500 divisible par 500 |
|
|
|
|||
|
|
|
|
N = … + 10 000D + 1000m + 100c + 10d + u N = 1000 ( …10D + m) + 100c + 10d +
u
(1000 a + du)k =
Si N = … CDU Alors Nk = … cdu
avec cdu
centaine, dizaine et unité de CDUk
4564
= 43 237 380 096 3 4564
= 142 657 607 172 096 23 4564
= 302 702 363 432 452 096 123 4564 = 232 299 784 284 558 852 096 |
|
|
|
|
|
|
|
|
|
||||
|
Propriété des carrés
de certains nombres Les puissances
des nombres terminés par les nombres suivants se terminent toutes par ces
nombres, et il n'y en a pas d'autres.
Propriété de ces
nombres Les carrés
de ces sept nombres se terminent tous par le nombre lui-même. Dans
l'ordre: 25, 625, 390625, 36, 5776, 141376, 87909376. |
Raison, par exemple
pour 76 Tout
nombre se terminant par 76 peut s'écrire 100A
+ 76 Exemple: 12376 = 123 x 100 + 76 Son carré devient: (100A + 76)² = 10000A² + 15200A + 5776 = 10000A² + 15200A + 5700
+ 76 = 100 (100A² + 152A + 57) + 76 =
100 B + 76 Le développement du carré redonne un nombre
du même type que le nombre initial; il se termine aussi par 76 et cela quels
que soit les autres chiffres placés devant; jusqu'à l'infini. |
|||
![]()
|
Suite |
|
|
DicoNombre |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/FORMATIO/Centaine.htm |
![]()