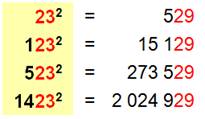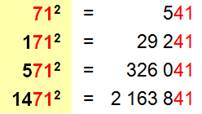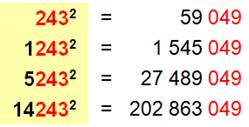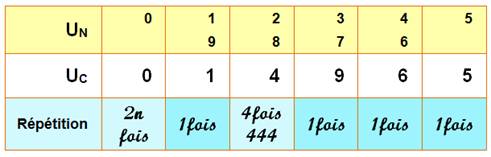
|
|||||||||||||||||||||||||||||||||||
|
CARRÉS – Chiffres finaux Quels sont les seuls
chiffres possibles à la fin des carrés? Nous nous intéressons
particulièrement à la répétition de chiffres finaux. Eh bien, ils ne se
répètent pratiquement jamais! (Sauf avec 0). Notations
|
|
|
||
|
Un nombre au carré Le nombre
n peut s'écrire: Son carré
devient:
|
Carré avec deux chiffres finaux
identiques (hors 00) Ce nombre s'écrit:
Une recherche systématique montre que la seule
possibilité est 11x = 44 avec quatre possibilités pour "du": {12,
38, 62, 88}. |
|
|
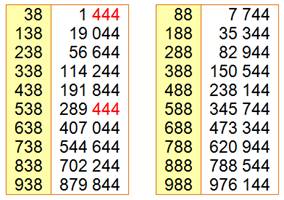
Exemples
Si un carré se termine par deux chiffres
identiques, ce sont 00 ou 44 et, pour 44, les dizaines-unités du nombre sont
{12, 38, 62 ou 88}. Voir Nombre 44 On trouve cette énigme sur Internet: Est-il
possible que le carré d’un nombre entier se termine par deux fois le même
chiffre impair ? La réponse est donc: non! |
||
|
|
||
|
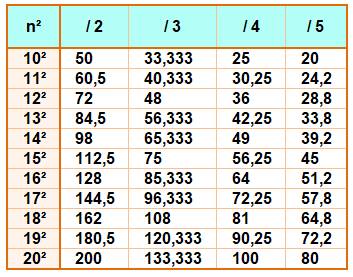
Le tableau montre qu'un carré divisé par: 2
=> quotient entier ou nombre en x,5 3
=> quotient entier ou nombre en x,333… 4
=> quotient entier ou nombre en x,25 5
=> quotient entier ou nombre en x,2 ou x,8 Exprimons
cela sous forme du reste de la division
(aussi appelé mod) |
Division des carrés par 2, 3,
4 ou 5
|
|
|
Restes de la division par k des carrés 2, {0, 1} 3, {0, 1} 4, {0, 1} 5, {0, 1, 4} 6, {0, 1, 3, 4} 7, {0, 1, 2, 4} 8, {0, 1, 4} 9, {0, 1, 4, 7} 10, {0, 1, 4, 5, 6, 9} 11, {1, 3, 4, 5, 9} 12, {0, 1, 4, 9} 13, {1, 3, 4, 9, 10, 12} 14, {1, 2, 4, 7, 8, 9, 11} 15, {1, 4, 6, 9, 10} 16, {0, 1, 4, 9} 17, {1, 2, 4, 8, 9, 13, 15, 16} 18, {0, 1, 4, 7, 9, 10, 13, 16} 19, {1, 4, 5, 6, 7, 9, 11, 16, 17} 20, {0, 1, 4, 5, 9, 16} |
Table des carrés mod k (restes de la division par k)
Ex: 3² = 9 = 1 x 5 + 4 => 4 mod 5 ou 3² = 9
= 1 x 6 + 3 => 3 mod 6 |
|
|
|
||
|
Dizaines Isolons la dizaine
et l'unité du nombre Le carré possède une structure
en deux termes dont le premier (100K) est terminé
par deux zéro. Si bien que, seul le terme h² détermine les unités et
dizaines du carré. |
N = 100 k + h
avec h =
et h2 = C = 10 000 k² + 100 x 2kh + h2 = 100 (100k²
+2kh) + h² = 100 K + h² |
|
|
Tout nombre de mêmes
unités et dizaines a un carré de mêmes
(autres) unités et dizaines. De plus, Le DU du carré est égal au du du nombre élevé au carré dont on
ne conserve que les deux derniers chiffres.
|
Exemples
|
|
|
Centaines Isolons la centaine, la dizaine et l'unité du
nombre et formons son carré. Le carré possède une structure
en deux termes dont le premier (1000P) est terminé
par trois zéro. Si bien que, seul le terme n² détermine les unités,
dizaines et centaines du carré. |
N = 1000 m + n
avec n =
et n2 = C = 106 m² + 103 x
2mn + n2 = 1000 (104
m2 +2mn) + n² = 1000 P +
n² |
|
|
Tout nombre de mêmes
unités, dizaines et centaines a un carré de mêmes
(autres) unités, dizaines et centaines. De plus, Le CDU du carré est égal au Cdu du nombre élevé au carré dont on
ne conserve que les trois derniers chiffres.
|
Exemples
|
|
|
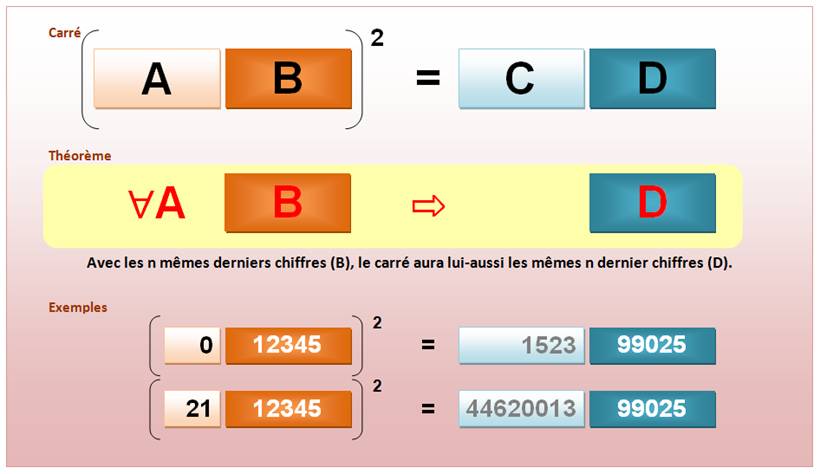
D'une manière
générale, des nombres qui ont les mêmes n
derniers chiffres ont des carrés qui ont les mêmes (autres) n derniers chiffres. En effet: (10n a + b)² = 10n k + b² Cette
propriété est vraie pour les cubes et toutes les puissances supérieures. En effet: (10n a + b)m = 10n
k + bm Ex:1235 =
28153056843; 51235 =
3528757217069081843. |
|
|
|||
|
Tout nombre dont l'unité est 0 a un carré qui se
termine par 0. |
UC = 0 |
02 =
0; 202
= 400 102 =
100; 2102
= 44 100 |
|
|
Bilan Tout carré terminé par 0 a un nombre pair de 0. (…0)2 = …00 Un carré peut comporter de nombreux zéros, mais
en quantité paire. (…0…0 n zéros)2 = …0…..0 2n zéros |
|||
|
|
|||
|
Tout nombre dont l'unité est 1 ou 9 a un carré
qui se termine par 1. |
UC = 1 |
1² = 1; 9² = 81 11² = 121; 19² = 361 |
|
|
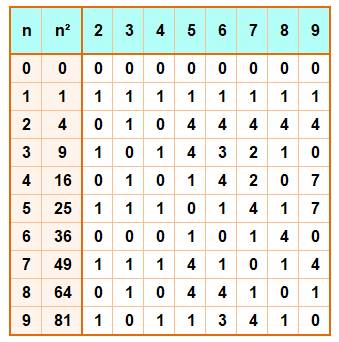
La propriété générale en action: voyons tous les
nombres inférieurs à 100 et terminés par 1 ou 9. |
Chiffres des dizaines relevés dans les
tableaux: D = {0, 2, 4, 6, 8} D est pair et, en aucun cas le
chiffre 1. |
|
|
|
Bilan Il n'existe aucun carré terminé par plus d'un
seul 1. n² = …11 n'existe pas Les carrés
terminés par un 1 sont suivis d'une dizaine paire. (…1)2 = … |
|||
|
|
|||
|
Tout nombre dont l'unité est 2 ou 8 a un carré
qui se termine par 4. |
UC = 4 |
2² = 4; 8² = 64 12² = 144; 18² = 324 |
|
|
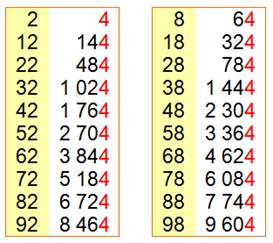
La propriété générale en action: voyons tous les nombres
inférieurs à 100 et terminés par 2 ou 8. |
Chiffres des dizaines relevés dans les
tableaux: D = {0, 2, 4, 6, 8} D est pair et, en particulier 4
pour 12, 62, 38, 88. |
|
|
|
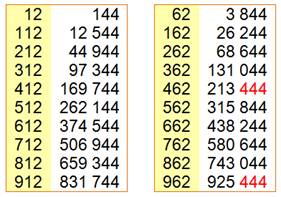
Propriété générale appliquée aux centaines dans
les quatre cas identifiés ci-dessus. |
Seuls cas avec 444: 38, 538, 462 et 962. Tous les nombres en …38, …538, …462 et …962 sont eux aussi terminés par 444. |
|
|
|
Bilan Il existe quatre types de carrés terminés par
…444. Il n'existe pas de carrés qui se terminent par
plus de trois quatre. Les carrés terminés
par un 4 sont suivis d'une dizaine paire. (…4)2 = … |
|||
Pourquoi pas plus de trois 4 à la fin d'un
carré ?
|
Si
N est un nombre carré alors ses facteurs sont carrés. Le premier (4) est
carré. Est-il possible que (2 500 x A + 1111) soit aussi un carré ? Non
! Car un carré ne se termine jamais par 11. |
|
|
|||
|
Tout nombre dont l'unité est 3 ou 7 a un carré
qui se termine par 9. |
UC = 9 |
3² = 9; 7² = 49 13² = 169; 17² = 289 |
|
|
La propriété générale en action: voyons tous les
nombres inférieurs à 100 et terminés par 3 ou 7. |
Chiffres des dizaines relevés dans les
tableaux: D = {0, 2, 4, 6, 8} D est pair et, en aucun cas le chiffre 9. |
|
|
|
Bilan Il n'existe aucun carré terminé par plus d'un
seul 9. n² = …99 n'existe pas Les carrés
terminés par un 9 sont suivis d'une dizaine paire. (…9)2 = … |
|||
|
|
|||
|
Tout nombre dont l'unité est 5 a un carré qui se
termine par 5. |
UC = 5 |
5² = 25; 115² = 13
225 15² = 225; 1115² = 1 243 225 |
|
|
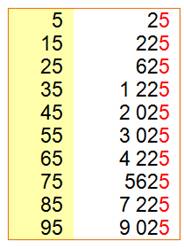
La propriété générale en action: voyons tous les
nombres inférieurs à 100 et terminés par 5. |
Tous ces carrés sont terminés par 25. |
|
|
|
Bilan Il n'existe aucun carré terminé par plus d'un
seul 5. n² = …55 n'existe pas Les carrés
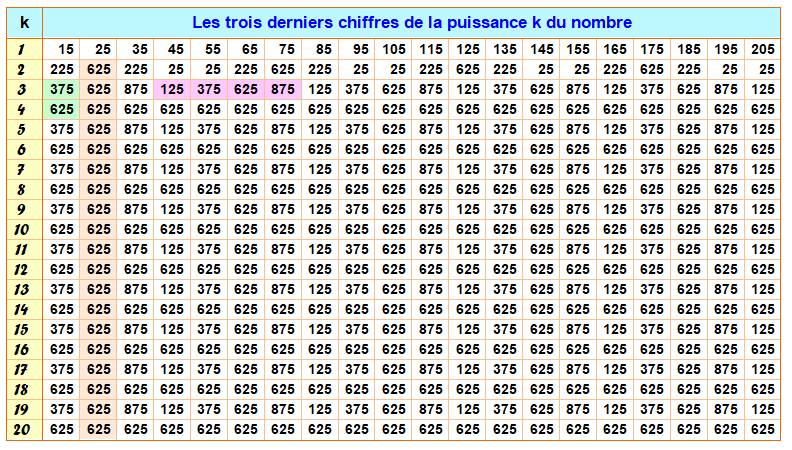
terminés par un 5 sont terminés par 25. (…5)2 = … Trois
derniers chiffres des nombres en 5 Les puissances des nombres terminés par 5
présentent des motifs répétitifs sur les chiffres des unités, des centaines et
desmilliers:
Voir Nombre
25 / nombre
55 / Cas du
nombre 51 |
|||
|
|
|||
|
Tout nombre dont l'unité est 4 ou 6 a un carré
qui se termine par 6. |
UC = 6 |
4² = 16; 6² = 36 14² = 196; 16² = 256 |
|
|
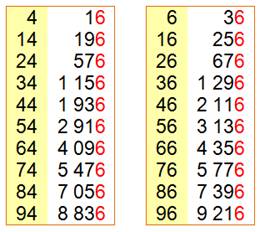
La propriété générale en action: voyons tous les
nombres inférieurs à 100 et terminés par 4 ou 6. |
Chiffres des dizaines relevés dans les
tableaux: D = {1, 3, 5, 7, 9} D est impair et, en aucun cas le chiffre 6. |
|
|
|
Bilan Il n'existe aucun carré terminé par plus d'un
seul 6. n² = …66 n'existe pas Les carrés
terminés par un 6 sont suivis d'une dizaine impaire. (…6)2 = … |
|||
|
Terminaison
des carrés
|
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/CarrTerm.htm |
