|
|||||||||||||||||||||||||||||||||||||||
![]()
|
INFINI – TRANSFINIS George Cantor est le mathématicien de l'infini ou des
différentes sortes d'infinis, les transfinis. |
|
|
|
|
|
|
|
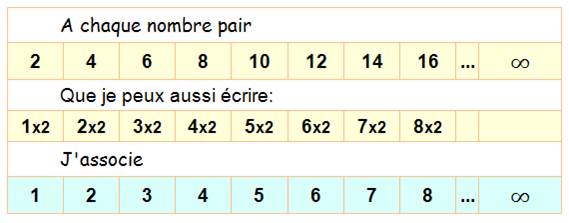
Est-ce que la quantité des nombres entiers est plus grande
que celle de leur carré. Il
est évident que la plupart des nombres ne sont pas des carrés. Alors leur
quantité devrait largement surpasser la quantité des nombres carrés. Et
pourtant, à chaque nombre on peut associer son carré. Conclusion: à l'infini, la notion de " plus grand,
plus petit ou égal " n'est pas applicable. |
Voir Paradoxe
|
|
|
|
On dit que tous ces
ensembles sont équipotents.
|
|
Voir Compter les nombres
|
|
|
|
Soit un hôtel ayant une infinité de
chambres occupées. Un nouveau client arrive. Que faire? Simple! On met le client 1 en chambre 2, le
2 en chambre 3, etc. La chambre 1 devenue libre est attribuée au
nouveau client. Maintenant, arrive une infinité de clients.
On met le client 1 en chambre 2, le client
2 en chambre 4, le client 3 en chambre 6, etc. Les chambres impaires deviennent
disponibles pour y loger les nouveaux venus. |
|
|
|
|
|
Voir Cardinal
|
|
|
|
|
|
Voir
procédé Zigzag.
|
|
|
|
|
|
Conclusion Il y a autant de points dans un segment
d'un milliardième de millimètre que dans un cube immense ou une hyper sphère
ou un volume de 7e dimension ou même de dimension infinie! |
|
|
|
|
|
Voir Hypothèse
du continu pour détails et nuances / Calculs avec
Aleph |
|
|
Il n'existe pas de plus grand infini ou
d'infini absolu. En effet: imaginons l'ensemble qui a le plus grand cardinal possible,
alors l'ensemble des parties de cet ensemble aurait un cardinal strictement
plus grand. Il est donc toujours possible de pousser plus loin l'infini. Rappel: soit un ensemble de deux
éléments {A, B}; son cardinal est 2 (la quantité d'éléments dans l'ensemble).
L'ensemble de ses parties {(A), (B), (AB)} a un cardinal 3. Cette propriété
est généralisable. Le cardinal d'un ensemble formé des parties d'un
ensemble est plus grand que le cardinal de cet ensemble. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/NbInfini/Transfin.htm |
![]()