Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 17/12/2023 M'écrire Brèves de Maths

INDEX Nombres (Classification) Types de nombres	Types de Nombres – Motifs
	Ulam	Chanceux d'Ulam	Mian-Chowla	Sylvester
		Hofstadter–Conway	Suites équilibrées	Dedekind

Faites un double-clic pour un retour en haut de page

Fonctions booléenne et Nombres de Dedekind Les nombres de Dedekind comptent les fonctions booléennes monotones croissantes à n entrées. Le neuvième nombre a été découvert en 2023
	Sommaire de cette page >>> Fonctions booléennes >>> Nombres de Dedekind	Débutants Logique Glossaire Logique

Fonctions booléennes		haut
Fonction booléenne Il s'agit d'une fonction logique dont les entrées sont vraies ou fausses (0 ou 1) et qui produit une sortie du même type (0 ou 1). Elles sont généralement réalisées par assemblages de portes logiques (ET, OU, …). Elles sont la base des systèmes d'automates comme les ordinateurs Précisément Les huit fonctions booléennes fondamentales sont des opérations logiques de base qui sont utilisées pour construire des propositions logiques et des circuits logiques en programmation informatique. Chaque fonction booléenne a une table de vérité qui spécifie comment les entrées sont combinées pour produire une sortie. En utilisant ces huit fonctions, il est possible de créer des propositions booléennes complexes qui peuvent être utilisées pour exprimer des conditions logiques dans les programmes informatiques, tels que des instructions conditionnelles, des boucles et des expressions de filtre. 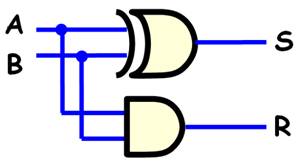Olivier Rocca	Additionneur deux bits S est la somme et R la retenue éventuelle. Voir Addition La fonction donnant S est un OU exclusif (sortie à 1 que si l'une ou l'autre des entrées est à 1). La fonction produisant la retenue est la fonction ET.
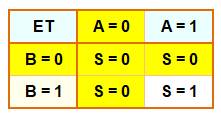
Fonction booléenne monotone Fonction telle que si une ou plusieurs entrées sont éteintes (fausses), la sortie est également fausse. La fonction ET est monotone S'il y a du "0" dans les entrées, la sortie ne peut être que "0". Une fonction booléenne monotone est une fonction dont la sortie, une fois passée à 1, ne revient jamais à 0, quel que soit l'ordre dans lequel les entrées sont inversées.	Avec la fonction logique ET, si l'une des entrées A ou B est fausse (0), la sortie S est fausse (0).
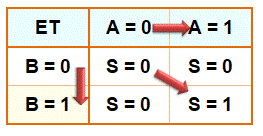
Fonction booléenne croissante Monotone : pour chaque combinaison de valeurs d'entrée, changer une entrée de faux à vrai ne peut que faire passer la sortie de faux à vrai (mais pas nécessairement) et non de vrai à faux.	Avec la fonction logique ET, si l'entrée A ou l'entrée B passe de 0 à 1, la sortie se "rapproche " du 1.

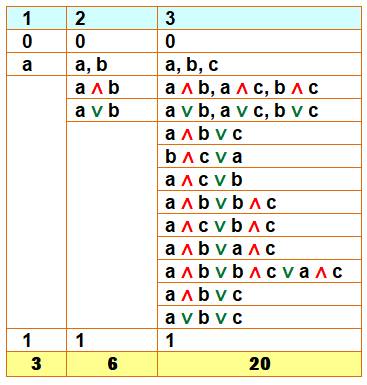
Tables des fonctions booléennes monotones à 1, 2 et 3 variables

Nombres de Dedekind		haut
Les nombres de Dedekind représentent les quantités de fonctions booléennes monotones a n variables.	Exemple pour n = 2 Il existe six fonctions booléennes monotones: La fonction f(x,y) = 0 qui ignore ses valeurs d'entrée et renvoie toujours 0; La fonction f(x,y) = 1 qui ignore ses valeurs d'entrée et renvoie toujours 1; La fonction f(x,y) = x qui ignore son deuxième argument et renvoie le premier argument ; La fonction f(x,y) = y qui ignore son premier argument conjonction logique f(x,y) = x ∧ y (ET); et La disjonction logique f(x,y) = x ∨ y (OU).
Liste D(0) = 2 D(1) = 3 D(2) = 6	2, 3, 6, 20, 168, 7 581, 7 828 354, 2 414 682 040 998, 56130437228687557907788, 56 130 437 228 687 557 907 788, 286386577668298411128469151667598498812366 OEIS A000372
Historique	1897 – Dedekind a proposé les cinq premiers. 1940 – Le cinquième par Church 1946 – Le sixième par Ward 1965 – Le septième par Church vérifié par Berman et Kölher en 1976 1991 – Le huitième par Wiedemann 2023 – Le neuvième simultanément par Chritian Jäkel et Lennart Van Hirtum et al.

Voir Brève 56-1109

Le cube à n dimensions		haut
Nombres de Dedekind On dispose de bille de deux couleurs: bleue et blanches. On considère un cube de dimension n Mettez le cube en équilibre sur un coin et attribuez une couleur à chaque coin. La règle: une bille bleue ne peut jamais apparaître plus bas qu'une bille blanche; mais elles peuvent être au même niveau. Combien de cubes coloriés différents sont possibles ? Pour un cube à n dimensions, ce nombre est le nième nombre de Dedekind d(n).	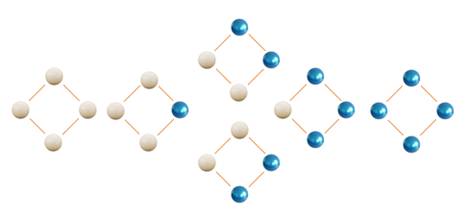Exemple avec n = 0 et 1 Exemple avec n = 2 (le cube de dimension 2 est le carré) Il existe six façons de disposer les billes blanches sans trouver une bille bleue plus à gauche qu'une blanche.

Exemple avec n = 3 (hypecube)

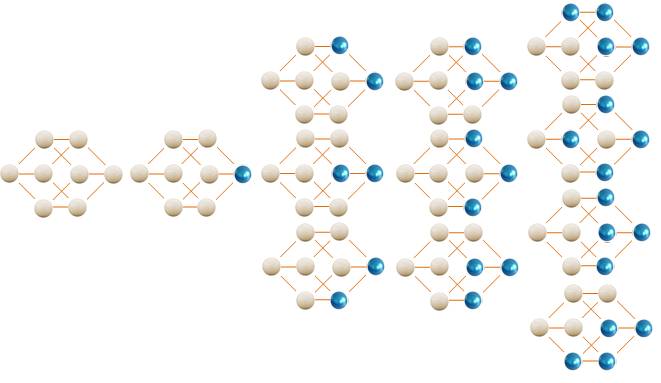
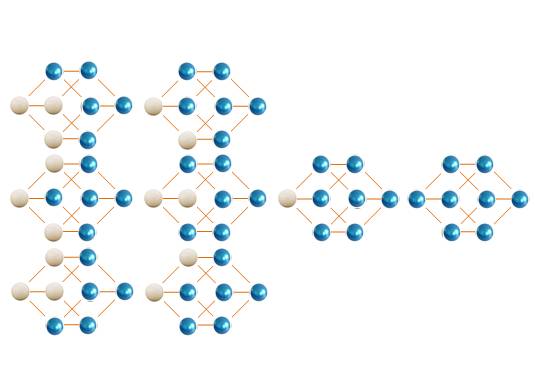
Les antichaines		haut
Notion de treillis Soit, par exemple, un ensemble de nombres : {1, 2, 3, …, n}. Cet ensemble peut être partitionné. On considère les sous-ensembles tels que les éléments des uns ne soient des éléments des autres. Ceux-ci sont appelés des antichaines. La quantité d'antichaines jusqu'à n est le nombre de Dedekind d'ordre n.	Antichaines d'ordre 2 et 3

Haut de page (ou double-clic)

Retour	Somme des numéros des maisons Maison du maire.
Suite	Logique – Cours Sommes égales de nombres triangulaires Nombre équilibrés Nombres balancés
Voir	Nombres chanceux d'Ulam Nombre chanceux d'Euler
Sites	Nombre de Dedekind – Wikipédia Ninth Dedekind Number Found by Two Independent Groups. Quata magazine – Rachel Crowell – August1, 2013
Cette page	http://villemin.gerard.free.fr/aNombre/TYPSEQUE/Dedekind.htm