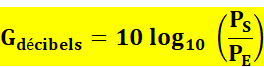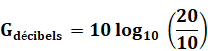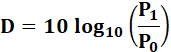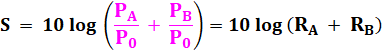NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/08/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Physique – Ondes
Débutants Général	SONS			Glossaire Général
INDEX Physique	Acoustique	Décibels	Musique
	Sommaire de cette page >>> Décibel >>> Gain et perte d'un circuit >>> Puissance et décibels >>> Oreille humaine >>> Doubler avec 3 dB >>> Amplificateurs en série >>> Amplificateurs en parallèle >>> Addition des décibels – Graphique >>> Addition des décibels – Valeurs >>> Addition des décibels – Formules >>> Électronique >>> Généralisation >>> Anglais

Décibels

Le décibel n'est pas une unité comme le mètre, mais la valeur (logarithmique) d'un rapport.

Que représentent les décibels et surtout comment les additionner. Les décibels utilisent une échelle logarithmique. Pourquoi? Parce que très souvent, une sensation ressentie par l'homme, comme le niveau sonore, varie comme le logarithme de l’excitation (loi de Weber-Fechner).

Deux sources sonores identiques ne provoquent pas une sensation double, mais la seconde ajoute un peu de bruit à la première. En décibels: 50 dB + 50 dB ne valent pas 100 dB, mais 53 dB. Cette page vous montre trois méthodes pour effectuer ce calcul: graphique, tableau ou formule.

L'oreille est capable d'entendre sur une dynamique de 130 à 140 décibels.

Décibel (dB)

Général Le décibel vaut 1/10 de bel (B) Graham Bell (1847-1922), physicien américain, inventeur du téléphone (1876) mais aussi de l’audiomètre. Unité de mesure destinée à évaluer principalement l'intensité sonore. Elle est utilisée aussi en physique ou en électronique. Le décibel est une valeur logarithmique qui exprime le rapport d'une grandeur (puissance) par rapport à une grandeur de référence. C'est donc une unité de mesure relative. Elle n'a pas de dimension. C'est une échelle de mesure. L’écart, mesuré en (déci) bels, entre deux valeurs est, par définition, égal au logarithme décimal du rapport de ces deux valeurs. Acoustique Le décibel est surtout utilisé en acoustique. L’intensité d’un son est mesurée sur une échelle dont le point de référence est la plus petite puissance sonore perceptible par l’oreille humaine: PRéférence = 10^-12 W / m^2 = 1pW.m^-2 L'oreille est capable de capter des sons sur une dynamique de pression de 20 µPa à 200 000 000 µPa (rapport 10^7). Cette dynamique exprimée en décibels va de 0 à -140 dB (= 20 log 10^7) Exemples 0 dB: un son à 4000 Hz commence à être audible. 20 dB: un son à 10 000 Hz commence à être audible. 45 dB: bruit d'une armoire électronique en fonctionnement. 70 dB: voix humaine lors d'une conversation. 120 dB: marteau piqueur ou avion au décollage. 150 dB: sirène d'alarme. 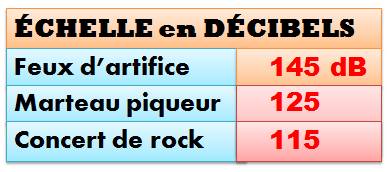À partir de 120 dB, le bruit peut provoquer des lésions irréversibles à l’oreille interne. Voir Son Note: Le décibel A dB(A) : la lettre A signifie que le décibel est pondéré pour tenir compte de la différence de sensibilité de l’oreille à chaque fréquence. Elle atténue les basses fréquences.

Gain et perte d'un circuit
Le décibel est utilisé pour comparer des grandeurs ayant de grandes dynamiques. En électricité, en acoustique, en traitement du signal, etc. Le décibel caractérise le rapport entre deux mesures; par exemple entre watts, volts ou ampères. Le décibel est la mesure d'un gain ou d'une perte entre un signal d'entrée et un signal de sortie à travers un circuit, comme typiquement un amplificateur.	Le circuit amplifie le signal d'entrée. Le rapport entre le signal de sortie et le signal d'entrée est un gain en cas d'amplification, c'est une perte dans le cas contraire.

Puissance (P en watts) et décibels
Plaçons-nous dans le cas où nous mesurons la puissance des signaux. L'unité est le watt. Le raisonnement sera légèrement différent pour les tensions (volts) ou les intensités (ampères). Un gain en décibels est égal dix fois le logarithme en base 10 du rapport des puissances. Ainsi avec un rapport de 100, le logarithme est égal à 2 et la valeur G en décibels est égale à 10 x 2 = 20 décibels. Avec une perte, les valeurs en décibels sont négatives. Dans le cas où le rapport n'est pas une puissance de dix, la valeur du logarithme est à chercher sur sa calculette. 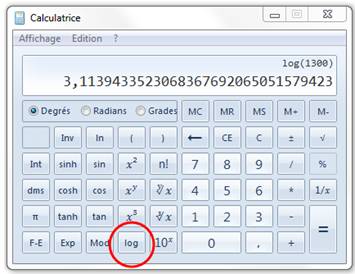Exemple: rapport des puissances = 1300 G = 31,13 décibels	1 W = 1 000 milliwatts (mW) 1 kW = 1 000 watts (W)

Oreille humaine et décibel "sonore"

Seuil d'écoute: 0,000 000 000 001 W/m²

Seuil de douleur: 1 W / m²

Rapport: 10¹²

Soit: 12 Bels ou 120 décibels

Conversion imaginée par Graham Bell (1847-1922), inventeur du téléphone.

Pour le son, sa pression sonore est comparée à une référence qui est la pression standard de l'air (20 micropascals). On admet qu'elle correspond au seuil d'écoute.

Voir Biologie – Index / Contemporains de G. Bell

Cas de 3 dB – Double
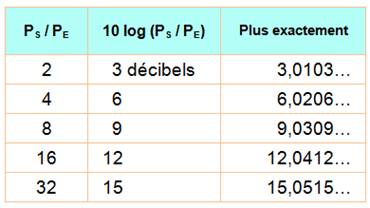
Exemple: PE = 10 mW et PS = 20 mW Lorsque le rapport de puissance est égal à 2, le gain est égal à 3 décibels (valeur couramment arrondie).
Avec un gain de puissance en puissances de 2, il est facile de calculer la valeur en décibels. Exemple: Un amplificateur de 9 décibels, avec un signal de 10 mW à l'entrée produira un signal de sortie de 10 x 8 = 80 mW. Si cet amplificateur est suivi d'un autre amplificateur de 3 décibels, le signal en sortie sera de 80 x 2 = 160 mW. L'ensemble des deux amplificateurs est équivalent à un seul de 9 + 3 = 12 décibels. En effet: 10 mW x 16 = 160 mW.

Amplificateurs en série
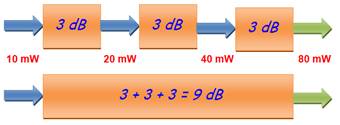
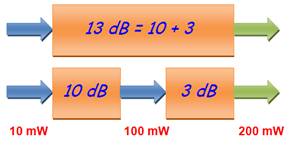
Nous venons de voir qu'un amplificateur de X décibels suivi d'un amplificateur de Y décibels est équivalent à un amplificateur de X + Y décibels. Ainsi trois étages à 3dB est équivalent à un seul de 9 dB. Un signal de 10 mW sortira de l'ensemble avec 80 mW. Nous savons que 3 dB c'est multiplier par 2, et 10 dB c'est multiplier par 10. Exemples: Un amplificateur de 13 décibels est équivalent à deux amplificateurs en série de 10 dB et de 3dB. 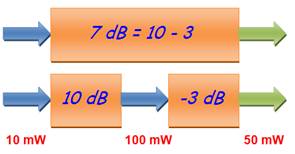Soit une puissance multipliée par 10 puis par 2; au total par 20. En effet: log 20 = 1,30103… Quelle est la puissance de sortie d'un amplificateur de 7 dB. Dans ce cas nous faisons 7 = 10 – 3. La puissance du signal est multipliée par 10 puis divisée par 2, soit multipliée par 5. En effet: log 5 = 0,69897000 …	Trois ampli de 3dB en série = 1 ampli de 9 dB Un ampli de 13dB = ampli de 10 dB puis ampli de 3 dB. Un ampli de 7dB = ampli de 10 dB puis ampli de -3 dB.

Voir Montage série et montage parallèle en électronique

Amplificateurs en parallèle
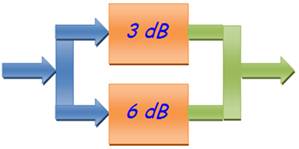
Ce cas est nettement plus délicat. Si une puissance de 10mW est injectée à l'entrée de l'ensemble, et en supposant que les impédances d'entrée des deux amplificateurs soient identiques, chacun d'eux ne "verra" à son entrée que la moitié de ces 10mW.
En RF (radiofréquences), un tel montage est équipé, en entrée, d'un "power splitter" ou coupleur -3dB, dont le rôle est précisément de diviser la puissance d'entrée en deux puissances égales (à la moitié de la précédente), lesquelles vont attaquer les deux amplificateurs. Ainsi, l'ampli de 3dB donnera 5 x 2 = 10 mW à sa sortie, tandis que celui de 6dB donnera 5 x 4 = 20 mW. Les puissances de sortie, additionnées dans un "power combiner" qui est l'exacte réplique du "splitter" de l'entrée, mais utilisé à l'envers, permettra d'obtenir 10 + 20 = 30 mW à la sortie de l'ensemble, dont le gain sera donc de 10 x log 3 = 4,8 dB. Il serait alors plus efficace d'utiliser seul l'ampli de 6dB ! Grand merci à Thiery A. pour cette explication professionnelle

La suite présente trois méthodes d'additions de décibels: graphique, tableau et calcul algébrique.

Addition des décibels - Graphique

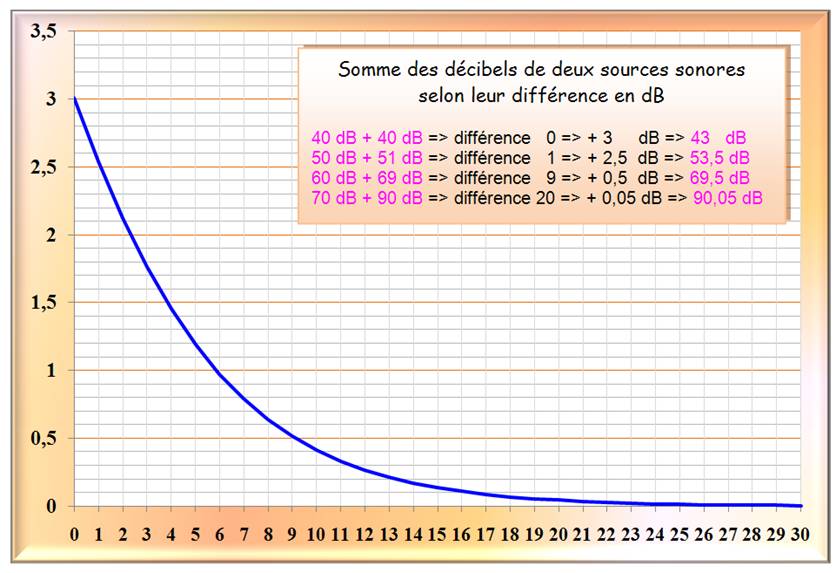
Cette courbe s'applique à deux sources sonores. Elle donne les dB supplémentaires à ajouter à la source la plus bruyante. S'il y a trois sources, procédez en cascade: calculez la source équivalente des deux d'entre-elles et recommencer avec celle-ci et la troisième. Procédez de même pour n sources. Exemples Trois sources de 40 chacune: 40 + 40 => 40 + 3 = 43 dB et 43 + 40 => 43 + 1,8 = 44,8 dB. Trois sources de 40, 42 et 44 dB => 40 + 42 => 44,1 dB et 44,1 + 44 => 47,1 dB

Addition des décibels - Valeurs
Ce tableau reprend explicitement les valeurs lisibles sur la courbe ci-dessus. N est la différence de dB entre deux sources, et S est la somme de ces dB. Lorsqu'on parle de niveau sonore, les trois décimales que donne cette table sont généralement superflues: le dB ou le demi-dB suffisent amplement.

Addition des décibels - Formules

La définition du décibel C'est le logarithme du rapport entre deux puissances: Exemples R = P1/P0 = 1000 => D = 10 log 1000 = 10 x 3 = 30 dB D = 30 dB => log(R) = 3 => R =10^3 = 1000 Dans le cas général où le nombre n'est pas une puissance de 10, il faudra une calculette ou le tableur de votre ordinateur. Somme des décibels Deux sources sonores de A et B décibels: => RA = 10^A/10 => RB = 10^B/10 Ajoutons les puissances (même dénominateur P0) et exprimons cette somme S en décibels: Note: Il s'agit bien de la somme des puissances PA et PB. Ne pas confondre avec la somme des logarithmes qui se traduirait par un produit: Exemples A = 40 dB et B = 44 dB S = 10 log10 (10^4 + 10^4,4) = 10 x 4,54 = 45,45 Pour information: 10^4 = 10 000 10^4,4 = 25 118,86 10^4 + 10^4,4 = 35 118,86 log10 (10^4 + 10^4,4) = 4, 545540463 … A = 40 dB, B = 40 dB et C = 40 dB S = 10 log10 (10^4 + 10^4 + 10^4) = 44,77 dB A = 40 dB, B = 42 dB et C = 44 dB S = 10 log10 (10^4 + 10^4,2 + 10^4,4) = 47,07 dB Calcul avec Mapple Voir Programmation Sources identiques 12 sources de 40 dB chacune S = 10 log10 (10^4 + 10^4 +…+ 10^4) = 10 log10 (12 x 10^4) = 10 log10 (12) + 10 log10 (10^4) = 10 log10 (12) + 40 dB = 10,79 + 40 dB n sources identiques créent une intensité sonore supplémentaire de 10 log10 (n) dB

De 90 dB à 180 dB

Question

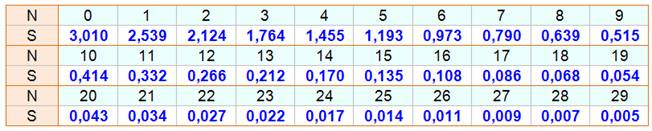
Combien de sources de 90 dB pour obtenir 90 dB de plus?

Réponse

On ajoute 10 log10 (n) dB avec n sources de plus.

On vérifie bien que 10 log10 (2) pour 2 sources = 3,010299957 dB (arrondi généralement à 3 dB).

Avec 3 sources on aurait 4,77 dB en plus. Etc.

Dans le cas demandé:

10log10(n) = 90

log10(n) = 9

n = 10^9 = 1 000 000 000

Il faut donc un milliard de sources de 90dB pour obtenir 180 dB.

Électronique

Un des problèmes de l'électronique, notamment en radio, consiste à capter un signal très faible et à le rendre suffisamment puissant pour actionner la membrane d'un haut-parleur et le rendre ainsi audible. L'amplification nécessaire se chiffre en puissance de 10 et le logarithme est d'un grand secours pour ne pas avoir à manipuler de très grands nombres. 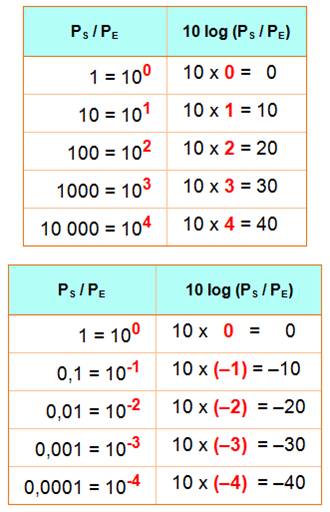Le coefficient d'amplification, rapport entre la puissance de sortie et celle d'entrée est le gain d'amplification qui se compte en décibels: G = 10 log10 (PS / PE) Exemple Si le rapport des puissances est de 1 million (10^6) Le gain est G = 10 log10 (10^6) = 10 x 6 = 60 dB En pratique: Puissance x 2 => gain de 3 dB Puissance x 4 => gain de 6 dB Puissance x 10 => gain de 10 dB Puissance x 100 => gain de 20 dB Etc.

Généralisation

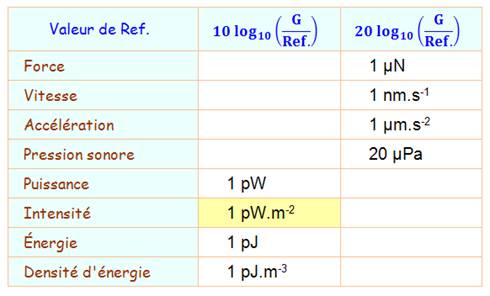
Idée générale Pour les spécialistes, il est courant de mesurer les tensions en entrée et en sortie, le gain est alors en 20 log. Ce nombre 20 intervient chaque fois que l'on utilise une grandeur plutôt que celle liée à son carré. C'est le cas pour U (tension) et P (puissance), liés par la relation P = U²/R. On se souvient que: 10 log (U²) = 2 x 10 log (U). Selon les grandeurs: 10 ou 20? et quelle référence? Formules en 10 log ou 20 log selon la grandeur (G) et indication de la grandeur de référence (Ref.). En jaune celle que nous avons indiquée pour l'intensité sonore.

Voir Unités, Préfixes des unités

ENGLISH CORNER

In the study of acoustics, calculations are mainly performed in decibels. Decibel: a logarithmic unit, symbol dB, used to express ratios of power, voltage current or sound intensity. Sound of any kind above 120 decibels causes incurable damage to hearing if exposure is prolonged. 10 log(2) = 3,010299957 but most people round it off to 3. A difference of 20 dB between two sounds means that the more intense one has 10 times the amplitude (100 times the power) of the softer. The human ear responds logarithmically and it is convenient to deal in logarithmic units in audio systems. The bel is the logarithm of the ratio of two powers, and the decibel is one tenth of a bel. The Bel was the amount a signal dropped in level over a one-mile distance of telephone wire.

Voir	Acoustique, son et sonars Unités Logarithmes Ondes Sons de la langue française Ultrason et jeunes
Site	Comparaison du volume de sources courantes de bruit – Wikipédia Les niveaux sonores – La note juste Decibel (Loudness) Comparison Chart – Diverses échelles de niveaux sonores
Cette page	http://villemin.gerard.free.fr/aScience/Physique/Decibel.htm