NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/10/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Analyse
Débutants Logarithme	LOGARITHME				Glossaire Général
INDEX Analyse	Introduction	Calcul	Exemples	Changement de base
		Propriétés	Décibel	EXPONENTIELLE
		Table	Maths	Historique
		Sommaire de cette page >>> Historique >>> Applications

LOGARITHMES & EXPONENTIELLES

HISTORIQUE

de logos = rapport, relation et arithmeticos = nombre

Lorsque l'astronomie s'est développée, les calculs nécessaires devenaient hypercomplexes. Comment simplifier les calculs? Les marins, demandeurs de simplification, suscitèrent l'invention des logarithmes.

Johannes Kepler (1571 – 1630) s'y est attaqué.

John Neper invente les logarithmes, une sorte particulière de nombres possédant une dynamique "compressée" telle que la multiplication de tels nombres se transforme en addition.

Voir Avant les log, les calculs avec la trigonométrie

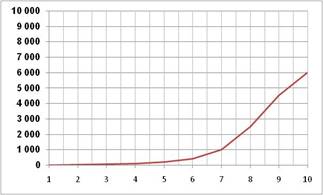
Idée du logarithme
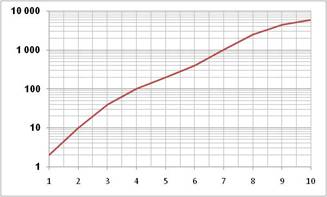
Échelle linéaire	Échelle logarithmique
Chaque tranche décuplée revêt la même importance. Permet de représenter des plages de nombres de grande dynamique. Les petites valeurs sont privilégiées par rapport aux très grandes. Transforme les opérations multiplications et divisions en additions et soustractions (non montré sur cette illustration).

Voir Les bases des logarithmes

ARCHIMÈDE
En voulant compter le nombre de grains dans un tas de sable, Archimède propose de représenter les grands nombres par des puissances de 10. Il ne passe pas loin des logarithmes avec son astuce de calcul du produit des grands nombres. Le système de notation des nombres de l'époque l'empêche de progresser et surtout de faire adopter ce genre d'idée.	Archimède (287-212 av. J.-C

BESOINS
Vers les années 1500 et 1600, on commençait à faire des calculs de plus en plus complexes avec de grands chiffres. C'était le cas des astronomes et des navigateurs. Car, ils utilisaient la trigonométrie sphérique. L'astronome Kepler (1571 - 1630), lui-même, avait tenté d'alléger les calculs; il utilisera les tables de Neper.	Simplifier les calculs de trigonométrie sphérique

Jost BÜRGI – Astronome suisse
En 1620, Bürgi, indépendamment de Neper, publie une table de log. Il avait choisi 1,0001 comme base. En 1588, pour faciliter ses calculs, Bürgi développe le premier système logarithmique connu. !!! Information à vérifier	Simplifier les calculs trigonométriques en astronomie

John NAPIER (1550 – 1617)
Il invente les logarithmes et, du coup, remplace les multiplications par des additions. La simplification est telle que cette découverte se propage à grande vitesse. En 1614, Neper publie la première table de log Plutôt un tableau de correspondance de sommes face à des produits Sa définition des logarithmes était plutôt géométrique et non selon une base. Il pose: x = 10^7 (1 - 10^-7)^y et donne le nom de logarithme à y y = log x	John Napier ou Neper, baron de Merchiston (près d'Édimbourg), mathématicien écossais. Étudiant, il fait partie du mouvement de la Réforme en Écosse. Livre: Mirifici logarithmorum canonis descriptio (1614) Il est le premier à utiliser le point décimal (virgule en France) pour exprimer des fractions Il invente la réglette de Napier, ébauche de la machine à calculer.

Table

Étant étudiant (années 1960), ma table de logarithmes (Laborde) ne comportait que cinq décimales et des indications d'extrapolation. C'était avant l'avènement des calculettes, bien entendu.

En 1845, Gray publiait des tables avec douze décimales, puis en 1867, une table avec 27 décimales.

MODERNES

Briggs (1561-1630) et Wright (1560-1615) calculent des tables de logarithmes décimaux et précisent comment les utiliser pour calculer des angles avec leur sinus ou tangente et réciproquement. En 1624, Briggs publie la table des logarithmes décimaux des 30 000 premiers nombres avec 14 décimales. Elle est complétée en 1628 par Adriaan Vlacq (1600-1167) avec une précision de 10 décimales. En 1661, Christiaan Huygens (1629-1695) identifie les logarithmes naturels (ou népériens). Gunta (1581-1626) et Wingate (1596-1657) inventent la règle à calcul. Mercator (1620-1687) et Newton (1642-1727) définissent les notions de fonctions logarithmes et exponentielles. En 1697, Gottfried Leibniz (1646-1716) met en évidence la fonction logarithme et sa fonction réciproque exponentielle. Puis, mise en place des techniques de calcul. Euler (1707 – 1783) travaille avec la constante "e".

APPLICATIONS
Interprétation de nombreux phénomènes: physiques biologiques économiques etc.	La constante e est la limite de (1 + 1/n)^n , ce qui explique sa fréquente apparition dans les problèmes mathématique, notamment des intérêts composés
Divers types de logarithmes selon la base utilisée et leur extension.	décimaux => physique binaire => informatique; théorie de la complexité népérien => maths complexe => maths (généralisation) discret => maths (généralisation)
Logarithmes décimaux.	Représentation => échelle logarithmique (tableur par exemple) Chimie => pH Acoustique => Décibel
Loi de Weber et Fechner ou loi physiologique	La perception d'un stimulus visuel ou auditif est proportionnelle au logarithme de l'intensité.
Magnitude des étoiles	En 1956, Norman Pogson (1809-1891) définit la magnitude apparente des étoiles: m = – 2,5 log10 (E / Ev) Avec E l'éclat de l'étoile et EV celui de l'étoile Véga. Une étoile qui paraît 100 fois moins brillante que Véga aura une magnitude apparente de 5, limite de l'observation à l'œil nu. On avait pris comme référence que la magnitude absolue (M) est égale à la magnitude apparente (m) pour une distance de 10 parsecs. Selon la distance D (en parsecs), la relation est la suivante: m = M + 5 (log10 D – 1) m = M + 5 log10 D – 5

Suite	Logarithmes – Propriétés Décibel
Voir	Exposants – Index Exposants et puissances Exponentielle Constantes Mathématiques Histoire – Index
DicoNombre	Ln 2 = 0,693… Ln 10 = 2,302 …
Site	Magnitude apparente – Wikipédia Magnitudes - Astronomy Online
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/LogaHist.htm