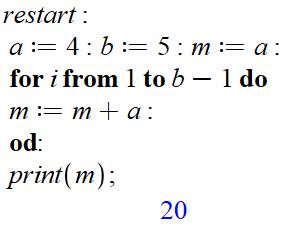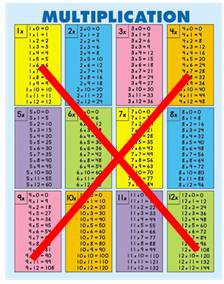
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/04/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	BASES de l'arithmétique
Débutants Nombres	MULTIPLICATIONS				Glossaire Nombres
INDEX CALCUL et autres pages sur la multiplication	Initiation		Avec les décimaux	Table 2, 5, 9
	Mental		Avec des négatifs	Table 3,4,6,7,8
	Par additions (sans table)		Sixième	Algébrique
		Sommaire de cette page >>> Multiplication par additions – Programmation >>> Multiplication avec additions et doubles – Approche >>> Grande multiplication – Disposition pratique >>> Grande multiplication – Optimisation >>> Bilan

MULTIPLICATION

sans tables

Méthode originale de poser la multiplication et de trouver le résultat en calculant simplement des doubles et des additions.

C'est-à-dire, sans les tables de multiplication, sauf celle très simple du 2.

Approche pas à pas de manière à comprendre le fondement de la méthode.

Voir Les quatre opérations – Junior

Multiplication paysanne (ou multiplication et division par 2

Exemple de multiplication par addition

Multiplication par additions répétées		haut
But Comment programmer une multiplication sans avoir l'instruction multiplication à disposition ?	Une multiplication est en fait une succession d'additions: 3 × 4 = 4 + 4 + 4 = 12
Programmation par boucles (Maple) Les deux nombres à multiplier sont a et b. Il faut réaliser b fois l'addition de a et mémoriser la progression de la somme dans m. Une boucle compte les additions: de 1 à b – 1 additions; la première étant le simple fait de dire que m = a en initialisation. Une fois toutes les additions réalisées, la somme est imprimée
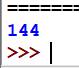
Programmation par méthode récursive (Maple) Une fonction (ici nommée procédure) est définie: elle exécute une multiplication. Le principe consiste à faire appel à la fonction elle-même pour effectuer toutes les multiplications à la file. Chaque addition est exécutée tandis que le nombre b décroit progressivement. Si ce nombre b atteint la valeur 1 alors la multiplication est terminée et on sort de la procédure. Version Python L'exécution de ce programme Python donne:

Voir Programmation – Index / Récursivité

Multiplication avec additions et doubles – Approche
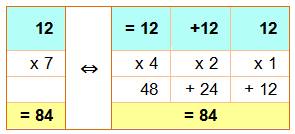
Dans les deux cas, on calcule les produits intermédiaires: 20 x 34 = 680 (le zéro étant implicite dans le décalage vers la gauche) et 1 x 34 = 34 Puis, on additionne.	Classique	Disposition linéaire
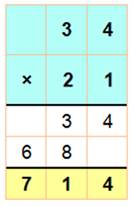
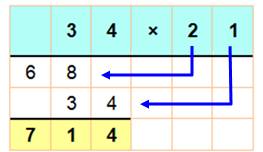
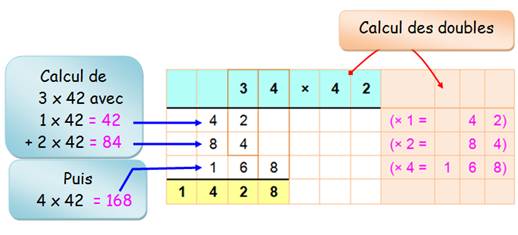
Méthode sans table On adopte la disposition linéaire. Puis, on transforme une multiplication en calcul de doubles (partie rose à droite) et d'additions (à gauche).	34 x 42 = 1 428
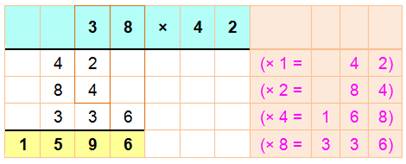
Deuxième exemple nécessitant de calculer un double supplémentaire pour atteindre 8 x 42.	38 x 42 = 1 596 (trois lignes de calcul)
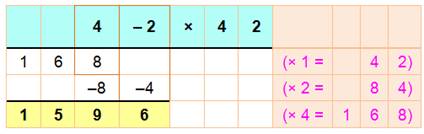
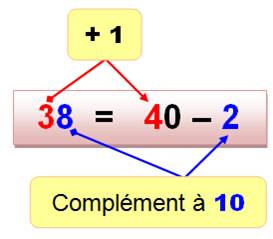
Même exemple, mais traité plus rapidement avec une soustraction. On transforme 38 en 40 – 2.	38 x 42 = 1 596 (seulement deux lignes de calcul)
Ce que nous avons fait: L'unité 8 devient son complément à 10, soit: 2; et La dizaine est incrémentée d'une unité: 3 devient 4.

Grande multiplication – Disposition pratique
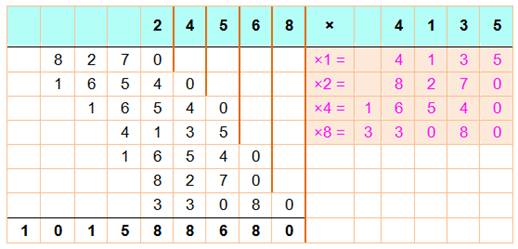
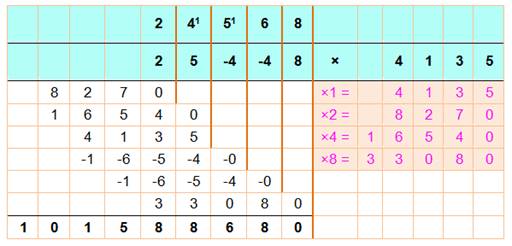
À droite, on calcule les doubles (y compris le x 1) de manière à piocher systématiquement dans le "rose". À gauche, on installe les nombres: directement s'il s'agit de 1, 2, 4 ou 8; ou sous forme de somme pour les autres. Notez bien les alignements. Le résultat découle naturellement de l'addition de tous ces nombres.	24 568 x 4 136 = 101 588 680 Cette disposition montre clairement les opérations (traits marons épais). Mais, évidemment, on peut adopter la disposition de la multiplication classique:
Aucune magie! C'est la multiplication classique pour laquelle, on remplace une multiplcation par 7 (par exemple) par la succesion de trois multiplications (par 1, par 2 puis par 4) et addition de ces trois nombres. L'addition comporte plus de lignes, mais ce n'est qu'une simple addition. Nous avons évité les calculs du type: 6 x 4 ou en encore 7 x 8 , etc. en ne calculant que des multiplications par 2. Là où s'exerce la "magie" de cette méthode, c'est avec l'optimisation, au prix d'une addition algébrique (additions et soustractions). Voir ci-dessous.

Grande multiplication – Optimisation
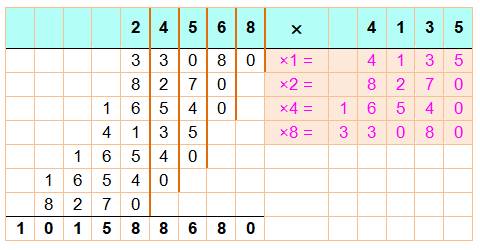
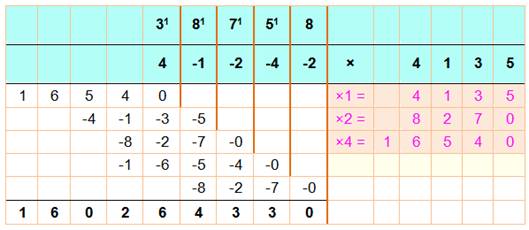
En utilisant la soustraction, dans ce cas, nous gagnons une ligne d'addition. Le calcul est un peu moins sympathique pour. transformer le multiplicande en une majorité de puissances de 2 (en plus ou en moins); et faire les soustractions qui conviennent sans faire d'erreurs sur les retenues.	24 568 x 4 136 = 101 588 680 Notez que le 5 ne peut pas se transformer en une puissance de 2. Obligation de passer par deux addition avec le 4 et le 1. Rassurez-vous en calculant: 25 000 – 400 – 40 + 8 = 24 568.
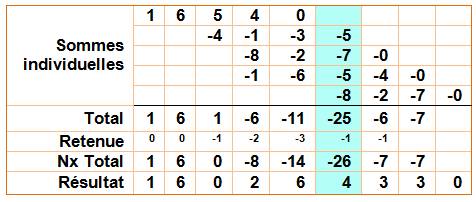
Autre exemple où, l'intérêt de la soustraction est manifeste. Somme explicitée ci-dessous	38 758 x 4 135 = 160 264 330
Calcul de la somme algébrique. Exemple pour la colonne bleue: total -25; avec la retenue venant de la colonne précédente: -1 donne un total de -26; le 6 en complément à 10 donne 4 et occasionne une retenue qui est ajoutée au 2 de la dizaine; et la retenue -3 est indiquée dans la colonne suivante.	Le calcul indiqué sur ce tableau peut être réalisé de tête. Cependant, sauf grande habitude, il est source d'erreur.

Bilan

La multiplication sans table est une manière originale de faire de très longues multiplications en n'utilisant que la table du 2 et en maitrisant les additions algébriques.

Merci à Anthony C. pour l'idée de cette page

Suite	Multiplication sans table – En divisant par 2 Multiplications visuelles Multiplication en sixième – Ce qu'il faut savoir Multiplications mentales – Méthode Trachenberg
Multiplication	Camion bien chargé (CM2) Multiplication et son symbole (x, point ou rien) Multiplications – Jeux Multiplications amusantes (niveau CE2) Multiplications de tous poils – y compris les TABLES Règle de trois Table de multiplications originales Table du 9 facile avec les doigts Tables de multiplication classique - apprentissage
Voir	Calcul mental – Index Débutants – Index Fractions Jeux – Index Preuve par neuf
Sites	Multiplier sans multiplications – Netmaths - Simon Lavallée – Vidéo
Cette page	http://villemin.gerard.free.fr/Calcul/Operatio/MultAdd.htm