|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Problème
de la table ronde de Dudeney Jamais le même COUPLE de voisins
Une
personne peut avoir le même voisin plusieurs fois, mais jamais les deux
mêmes. |
Anglais: The round table problem / Dudeney' round table
problem
No person shall ever have the same TWO neighbours TWICE
|
Problème abordé par Dudeney en 1905 et publié en 1917 dans
son livre: Amusements in mathématics (problem 273 – No person shall ever have
the same two neighbours twice). Ce
problème est résolu pour n pair et sans solution au-delà des impairs
supérieurs à 41. En 1899, Charles Judson s'était posé le même genre de
problème avec sept personnes qui devaient rester en vacances autant de jours
qu'ils pouvaient s'assoier sans retrouver le même couple
de voisins. Ils passèrent quinze jours de vacances ensemble. |
|
|
||
|
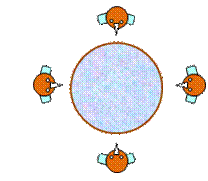
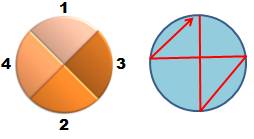
Il
n'existe qu'une seule possibilité pour disposer trois personnes autour d'une
table. On peut bien entendu inverse 2 et 3, mais les voisinages seront les
mêmes. Le
circuit hamiltonien est unique avec le triangle. La
quantité est également égale à: |
|
|
|
|
||
|
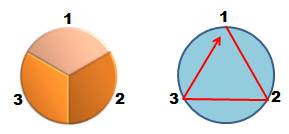
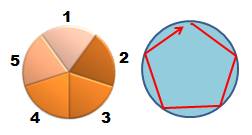
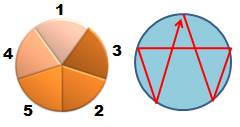
Trois
possibilités comme le montre les trois chemins hamiltoniens.
La
quantité est également égale à: Note: parmi les six permutations de (2, 3, 4), nous
en avons sélectionné trois: (1234, 1243, 1324). Les trois autres (1342, 1423,
1432) offrent aussi une configuration recevable. En fait, c'est la même en
tournant autour de la table dans l'autre sens; d'où le ½ dans la formule. |
|
|
|
|
||
|
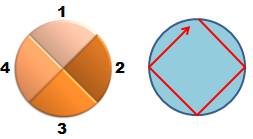
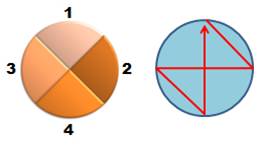
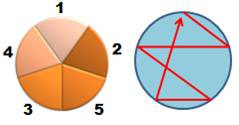
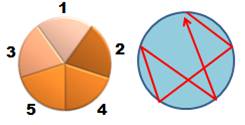
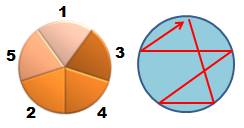
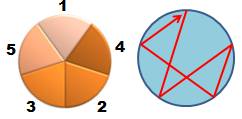
Six
possibilités comme le montre les six chemins hamiltoniens sélectionnés. La
quantité est également égale à: Note: parmi les 4! = 24 permutations de (2, 3, 4),
seules six (et six autres par rotation inverse) sont retenues. Le second
groupe de 2 x 6 forment également une solution recevable. Tout est dans le
choix des six élus, même s'il existe quatre possibilités. |
|
|
Voir
Cas de six personnes
Quantité (Q) de dispositions pour n
personnes
|
n |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Qmax |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
|
Qvérifiées |
1 |
3 |
6 |
7 |
11 |
14 |
23 |
Les nombres Qmax = ½ (n – 1) (n
– 2) sont les nombres
triangulaires
Notez le motif
répétitif du type: 15 = 10 + 5
Formulation générale du problème
|
Telle que Dudeney le formulait: Placer
les mêmes n personnes autour d'une table ronde en ½ (n – 1) (n – 2)
occasions, de façon telle aucune personne ne rencontre jamais les deux mêmes
voisin deux fois. Équivalence en théorie des graphes Trouver
un ensemble de cycles hamiltoniens dans un graphe complet K, tel que tout
2-chemins (chemin de longueur 2) appartienne à exactement un des cycles. Un
tel ensemble est dit ensemble de Dudeney. |
Voir Graphe

Source: Dudeney’s round table problem – Athabasca University
Library
et aussi Dudeney's round table problem – Katherine Heinrich et
al
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()