|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
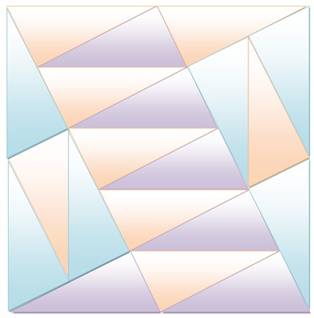
Carré divisé en cinq Avec une simple règle comment diviser le carré en
cinq parties rigoureusement égales. Énigme classique, étudiée pas à pas. |
Voir Brève
906
|
|
|
|
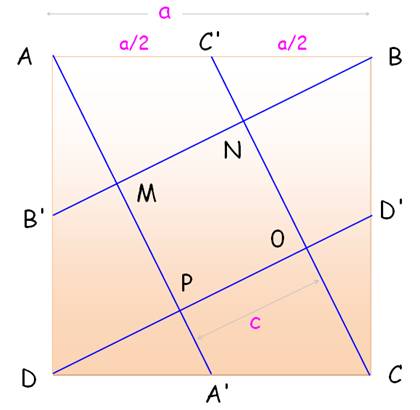
La découpe résulte du tracé des pseudo-médianes: droites issues
d'un sommet et rejoignant le milieu du côté opposé.
Si : cc = b = ½ c, alors: Aire du carré central = cc² Aire du triangle = ½ b.c = ½ cc.(2cc) = cc² On aura aussi: a = b Démonstration ci-dessous |
|
|
|
|
|
|
|
|
|
|
|
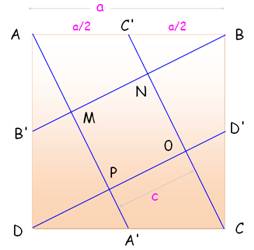
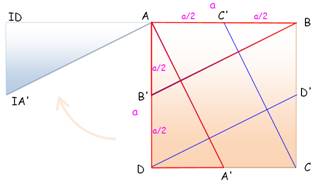
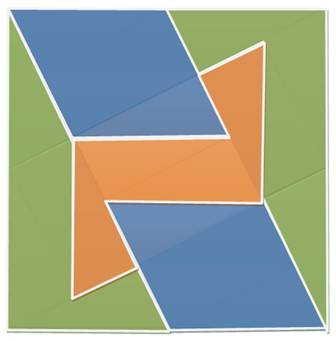
1. MNOP est un losange >>> 2. MNOP est un carré >>> 3. Partage du segment BB' >>> 4. Aires (MNOP) = Aire (ABM) >>> |
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
B'M = ½ DP = c/2
|
|
|
|
|
||
|
A(ABM) = ½ AM x MB
|
A(MNOP)
= MN² = c²
5 c² = a² a = c |
|
|
|
|
|
|
|
![]()
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()