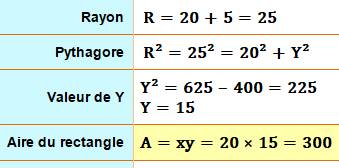|
Édition du: 04/02/2024 |
|
INDEX |
QUADRILATÈRES – Compter |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
RECTANGLES Jeux, défis, énigmes |
||
|
|
Sommaire de cette page >>> Rectangle entouré de
carrés >>> Aire du rectangle
dans le triangle rectangle >>> Aire du rectangle
dans un quart de cercle (1/2) >>> Aire du rectangle
dans un quart de cercle (1/2) >>> Rectangle coupé en
deux parties égales >>> Rectangle partagé –
Énigme |
Débutants Glossaire |
Solution
en brève 756
|
|
||
|
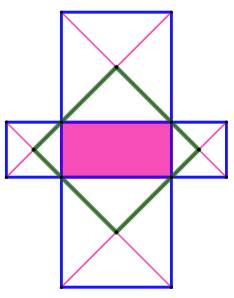
Propriété Un
rectangle, flanqué de quatre carrés. Le
quadrilatère vert dont les sommets sont les centres des carrés est lui-même
un carré. Démonstration Les
diagonales du carré se coupent à angle droit: les angles aux sommets sont
droits. Les
demi-diagonales des carrés sont de même longueur. Leur assemblage pour donner
les côtés du carré sont également de même longueur. Le
quadrilatère avec quatre angles droits et des côtés de même longueur est un
carré. |
|
|
|
|
||
|
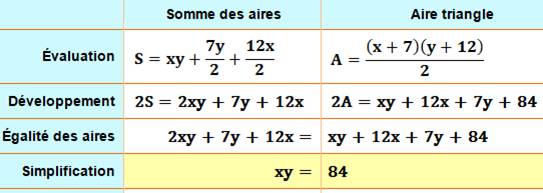
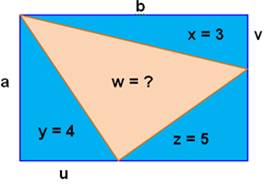
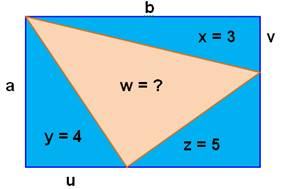
Énigme Un
triangle rectangle et un rectangle inscrit. On ne connait que les deux
mesures indiquées. Quelle
est l'aire du rectangle ? Solution On
compare l'aire du triangle complet à la somme des aires du rectangle et des
deux petits triangles. |
|
|
|
|
||
Voir Brève
718
|
|
||
|
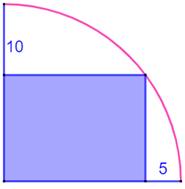
Énigme Un
rectangle inscrit dans un quart de cercle. Solution
|
|
|
Voir Brève
743
|
|
||
|
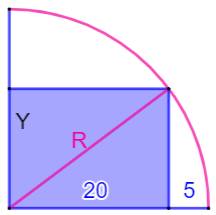
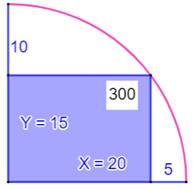
Énigme Un
rectangle inscrit dans un quart de cercle. Solution
|
|
|
|
|
|
|
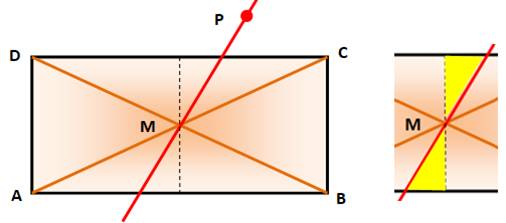
Problème Partager le rectangle ABCD en deux parties
de surface égale à partir d'un point P donné. Construction Tracer les diagonales pour obtenir le point
milieu M. Tracer la droite PM qui partage le rectangle en deux parties
égales.
Le
zoom à droite montre que les triangles jaunes son égaux (isométriques). L'un
compense l'autre avec effet de conserver des aires égales. Théorème Dans
un rectangle, toute sécante passant par le point milieu partage celui-ci en
deux surfaces égales. Voir Constructions – Index |
|
|
|
|||
|
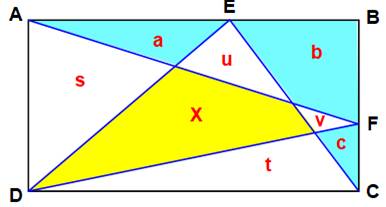
Énigme Un
rectangle ABCD et deux points E et F quelconques sur AB et BC. Que
peut-on dire de la surface jaune par rapport
à celles en bleu ? Remarque L'aire d'un triangle inscrit dans un rectangle
(comme ADF ou DEC) est égale à la moitié de l'aire (R) du rectangle. |
|
||
|
Solution |
Aire de ADF Aire de DEC Aire du rectangle |
X
+ s + v = R/2 X
+ u + t = R/2 X
+ s + v + u + t + a + b + c = R |
|
|
|
En remplaçant |
X + (R/2 – X) + (R/2 – X) + a + b +
c = R a + b + c – X = 0 X = a +
b + c |
|
Voir Brève
342
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()