|
||||||||||||||||||||||||||||
![]()
|
CERCLE Cordes, sécantes, puissance AM . MB = A'M . MB' Propriété que l'on retrouve
avec:
|
|
|
|||
|
Ils sont semblables (on dit aussi homothétiques).
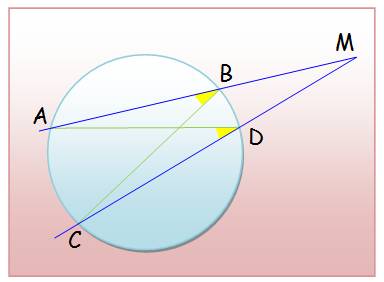
MA.MB = MC.MD
|
Les angles en
jaune interceptent le même arc, ils sont égaux. Les triangles
MAD et MCB sont semblables, mais attention de comparer leurs proportions dans
le bon ordre. Réciproque (de Feuerbach) Si MA.MB =
MC.MD alors les quatre points A, B, C et D sont situés sur une cercle. Ils
sont cocycliques. |
||
|
|
||
|
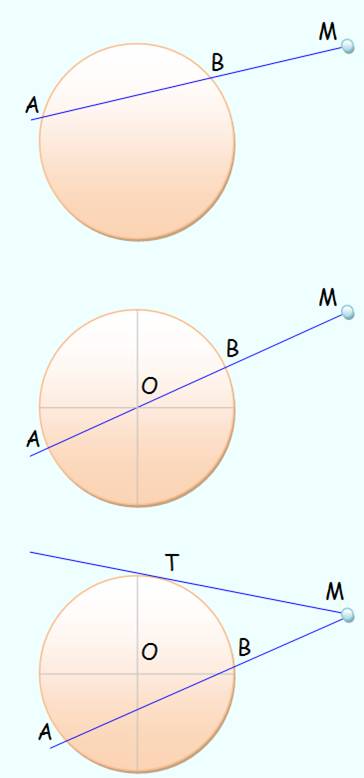
Puissance
La
sécante passe par O
MA.MB = (MO + OA) (MO – OB) = (d + R) (d –R) = d² - R² La
sécante est tangente
MA.MB = MT²
|
|
|
|
|
||
|
|
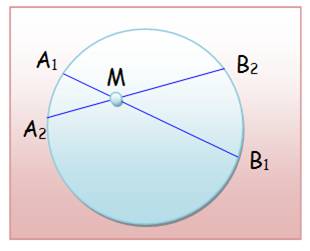
A1 M . M B1 = A2 M . M B2 |
|
Voir Théorèmes
des cordes sécantes et sa démonstration / Application
/ Autre application (calculs)
Énigme des
deux cercles (Brève 921)
|
|
|||
|
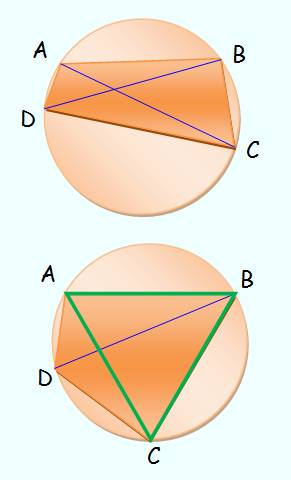
Théorème
de Ptolémée
AB = BC = AC
AB . CD + AB . DA = AB . BD CD
+ DA = BD Voir Démonstrations |
|
||
Voir Calcul
de l'aire du quadrilatère inscriptible
|
|
||||
|
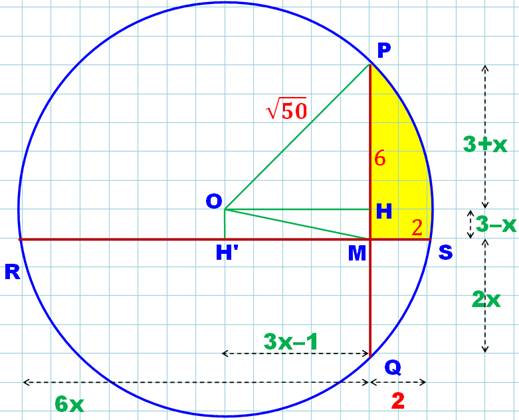
Une démonstration très originale reposant sur le théorème des cordes
puis sur un doublé du théorème de Pythagore.
On sait que MS = 2 et MP = 6.
Les
indications en vert vont être expliquées.
Le facteur
deux est inutile car il sera question de diviser MQ par 2. |
|
|||
|
Démarche |
3) Calcul de OM avec Pythagore dans OHM. 2) Donc, calculer d'abord les longueurs de OH et HM. 1) Pour OH, appel à Pythagore dans OHP. |
|||
|
|
MQ = 2x PQ = 2x + 6 HP = x + 3 HM = (x + 3) – 2x = 3 – x |
|||
|
PM x MQ = RM x MS 6 . 2x = RM .
2 RM = 6x |
||||
|
|
RS = 6x + 2 H'S = 3x
+ 1 OH = H'M
= 3x + 1 – 2 = 3x – 1 |
|||
|
|
OP² =
OH² +
HP² 50 = (3x
– 1)² + (x + 3)² = 9x² – 6x + 1 + x² + 6x + 9 = 10x² + 10 5 = x² +
1 x² = 4 x = 2 |
|||
|
|
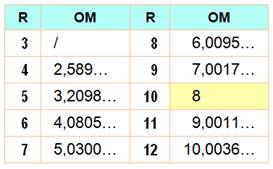
OM² =
OH² + HM² = (3x – 1)² + (3 – x)² = (3.2 – 1)² + (3 – 2)² = 5² + 1² = 26 OM = |
|||
|
Notez qu'il serait plus plaisant de poser problème
avec R = 10 qui conduit à une valeur entière pour OM (= 8). |
|
|||
![]()
![]()