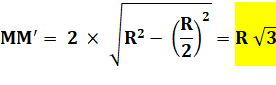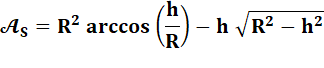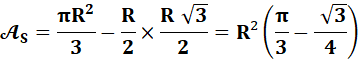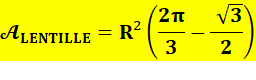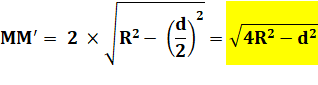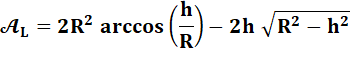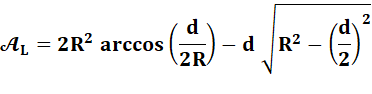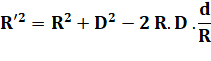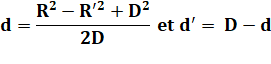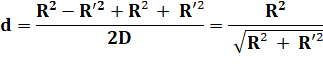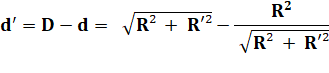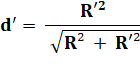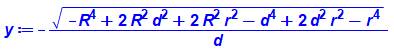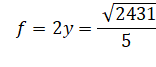|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Deux CERCLES Aire de la lentille d'intersection
Le cas général sera abordé
après exposition de quelques cas particuliers, plus simples. Si on connait l'aire de la lentille,
on connaît, par différence, l'aire de la lunule
associée. La lentille particulière
avec les cercles passant par le centre de l'autre est appelé Vescica
Piscis ou Mandorle. |
|
|
||
|
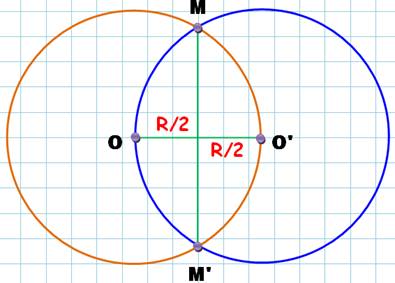
Lentille symétrique dite Mandorle
ou Vesica piscis Deux
cercles de rayon R. L'un
passe par le centre de l'autre. Alors:
OO' = R Longueur du segment MM'
Aire de la lentille = 2 x Aire du segment MO'M'. Aire du segment:
Avec: h, la
hauteur du segment = R/2 R² – h² = R² – (R/2)² = 3R²/4 Arccos (h/R) = arcos(1/2) = 60°=
|
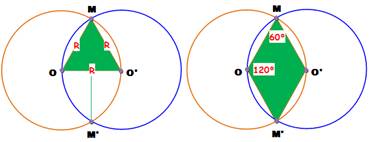
Les triangles OMO' et OM'O' sont équilatéraux MO = MO' = OO' = R;
Angle MOO' = angle
MO'O = angle OMO' = 60°. |
|
|
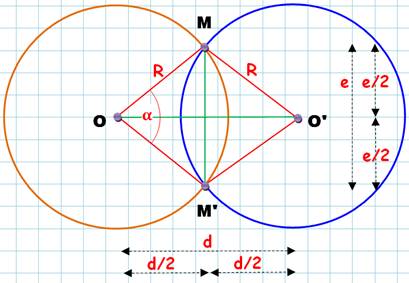
Lentille symétrique d'inter-centre
quelconque Deux
cercles de rayon R. Les
centres sont distants d'une longueur d. Longueur du segment MM'
Exemple: R = 5 et d = 8 alors MM' = 6 Aire de la lentille La figure
reste symétrique et l'aire de la lentille est égale à deux fois celle du
segment.
Avec h =
d/2
|
Application numérique R = 5 et d = 8 avec
arccos 8/10 = 0,6435 … radian
|
|
|
||
|
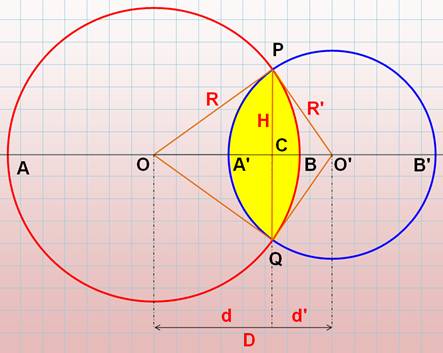
Lentille asymétrique On ne donne pas de
formule finale. En pratique, suivre les étapes de calcul. Deux
cercles de rayon R et R'. Les
centres sont distants d'une longueur D. Longueur PQ >>> L'aire de la lentille est égale à la somme de deux segments. |
|
|
|
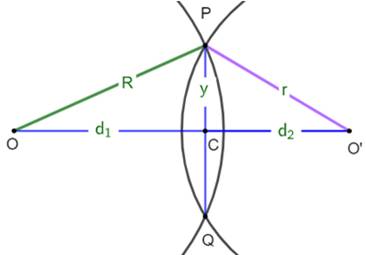
Calcul de
d et d' |
Calculer d, cela revient à calculer l'abscisse du pied
de la hauteur PC du triangle quelconque OP0' |
|
|
La loi des cosinus en
général puis,
appliquée à notre cas |
|
|
|
Soit la
valeur de d et d'. |
|
|
|
Segment –
Formule générale |
|
|
|
Dans les
triangles rectangles OPC et O'PC |
H² = R² – d² = R'² – d'² |
|
|
Segment
lié au cercle (O, R) |
|
|
|
Segment
lié au cercle (O', R') |
|
|
|
Application numérique (voir figure) R = 6,6 R' = 4,7 D = 8 |
d =
5,3418750 d' =
2,6581250 H =
3,876128 As =
6,637 A'S = 11.,117 AL = 17,754 |
|
|
Cas où l'angle
d'intersection est droit |
|
|
|
Deux
cercles de rayon R et R'. Les
centres sont distants d'une longueur D inconnue. On sait
que l'angle OPO' est droit. |
D² = R² + R'² |
|
|
Valeur de
d et d'. |
|
|
|
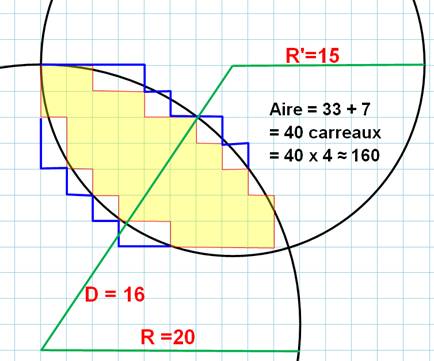
Application numérique Avec les
mêmes formules que ci-dessus R = 20 R' = 15 |
D = 25 d =
16 d' =
9 H =
12 As =
6,637 A'S = 65,40 AL = 166,04 |
|
|
Vérification graphique Remarquez
la position des cercles pour obtenir facilement l'angle de 90° à
l'intersection. Le
graphique donne 160 pour un calcul à 166. |
|
|
|
Longueur du segment MM' pour la
lentille asymétrique Autant le
dire tout de suite, le calcul de la longueur est complexe et passe par la
résolution d'une équation du quatrième degré
Nous
avons d en fonction de y; avoir y en fonction de d passe par une double
élévation au carré qui nous mène au quatrième degré pour y. Tous
calculs faits:
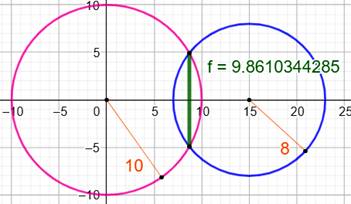
Exemple: R = 10, r = 8; d
= 15
f =
9,8610344284898… |
Notations
Exemple
|
|
|
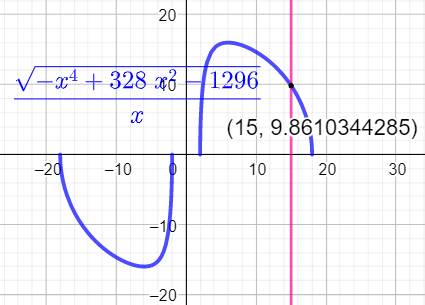
Graphe de f en fonction de d, Le trait rose montre le cas d = 15, vu dans l'exemple ci-dessus. Si d est trop grand (> 18): les cercles s'éloignent l'un de l'autre
et pas d'intersection. Si d est trop petit (< 2):
le cercle bleu est intérieur au rose et pas d'intersection. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Lentille.htm |
![]()