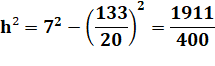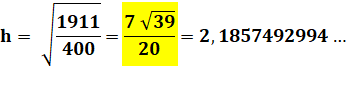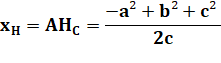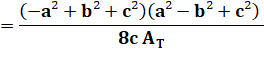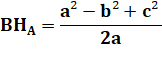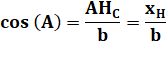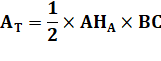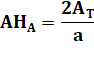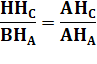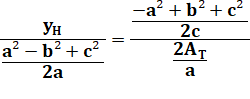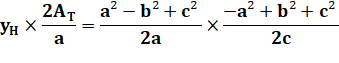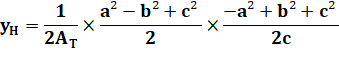Orientation Glossaire	Atlas / Géométrie / Figures / Droites Médiane / Médiatrice / Bissectrice
Débutant DicoMot DicoNombre	HAUTEUR d'un triangle ORTHOCENTRE
	Sommaire de cette page >>> Définition >>> Propriétés >>> Orthocentre >>> Anglais	Section avancée >>> Construction du triangle avec orthocentre donné >>> Coordonnées de l'orthocentre

L'ingénieur et les directeurs

Mission: mesurer la hauteur d’un mât.

Le directeur général, le directeur industriel et le directeur qualité montent sur une échelle et déploient un mètre-ruban, sans succès.

Un ingénieur passe, couche le mât et le mesure.

Sarcasme des directeurs: voilà bien un ingénieur! On cherche la hauteur, il nous donne la longueur!

Voir Pensées & humour

Définition	Hauteur d'un triangle: droite issue d'un sommet du triangle et perpendiculaire au côté opposé.
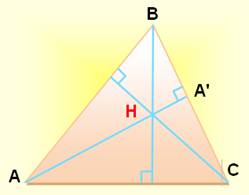
Triangle	Les hauteurs du triangle sont concourantes en un point H dit orthocentre du triangle. Le point A' est appelé le pied de la perpendiculaire. Voir Points du triangle

Propriétés

L'orthocentre ne se trouve à l'intérieur du triangle que si les trois angles du triangle sont aigus; un seul angle obtus est l'orthocentre est à l'extérieur du triangle. L'orthocentre d'un triangle rectangle est en fait le sommet de l'angle droit. Les hauteurs du triangle sont les médiatrices de son triangle quadruple. Cette propriété permet d'affirmer que les hauteurs sont concourantes dès que l'on a démontré que les médiatrices sont concourantes. Voir Démonstration

Orthocentre

Orthocentre Point de concours des trois hauteurs d'un triangle. Suite >>> Point de concours des quatre hauteurs d'un tétraèdre lorsqu'elles se rencontrent: tétraèdre orthocentrique. Groupe orthocentrique de points De quatre points dans un plan: une droite passant par deux d'entre eux est perpendiculaire à celle qui passe par les deux autres. Équivalent à la situation dans le triangle des droite AB et CO (O étant l'orthocentre du triangle). De cinq points dans l'espace: avec les quatre sommets d'un tétraèdre orthocentrique et son orthocentre: une droite passant par deux d'entre eux est perpendiculaire au plan formé par les trois autres.

Anglais

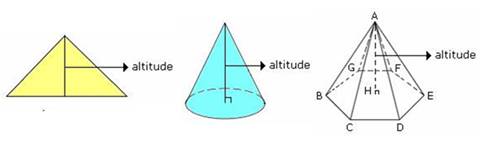
Altitude of a triangle: a line through one vertex of a triangle and perpendicular to the opposite side. The three altitudes of a triangle are concurrent at the orthocenter (US) or orthocentre (UK). Often used in the area of a triangle as the height. Altitude of a geometric figure is the shortest distance from its top (vertex) to its opposite side (base). This opposite side of the vertex is called the base of the altitude, and the point where the altitude intersects the base (or its extension) is called the foot of the altitude. The length of the altitude is the distance between the base and the vertex. The three altitudes intersect in a single point, called the orthocenter of the triangle. The orthocenter lies inside the triangle if and only if the triangle is not obtuse. The three vertices together with the orthocenter are said to form an orthocentric system.

En savoir plus

Calcul des hauteurs rationnelles d'un triangle Constructions élémentaires: hauteurs Distance à l'orthocentre Éléments remarquables du triangle Géométrie – Index Hauteurs – Propriétés Hauteurs concourantes – Démonstrations Hauteurs du triangle: propriétés et démonstrations Orthocentre – Démonstrations Résolution du triangle via la hauteur Triangles Triangles – Index

Section avancée*

Hauteur rationnelle
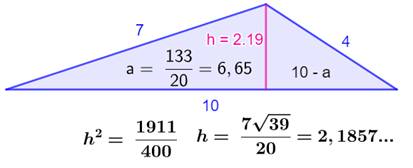
Un triangle dont les côtes sont des nombres entiers. Une des hauteurs mesure environ 2,19. On voudrait une valeur exacte. Comment s'y prendre ? La hauteur est mitoyenne de deux triangles rectangles.
Théorème de Pythagore:	h² + a² = 7² h² + (10 – a)² = 4²
Différence	h² + 100 – 20a + a² – h² – a² = 4² – 7² 100 – 20a = 33 a = 133 / 20 = 6,65
Calcul de h La valeur du carré est une fraction La valeur de h est une expression avec fraction et radical

Voir Trigonométrie rationnelle (d'autres exemples de calculs)

Construction du triangle avec orthocentre donné
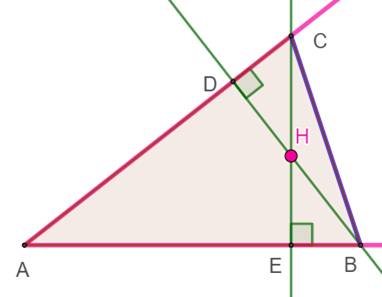
On donne un des angles du triangle et son orthocentre. Compléter le triangle. Construction 1. Angle BAC donné. 2. Orthocentre H donné. 3. Perpendiculaires passant par H à chacun des côtés de l'angle. Intersections B et C 4. Le triangle ABC est le triangle cherché. Le point H est bien l'intersection de deux hauteurs (HD et HE), c'est l'orthocentre du triangle ABC. On sait que la troisième hauteur passe également par le point H.

Coordonnées de l'orthocentre
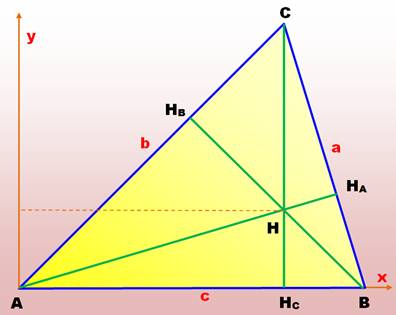
Quelles sont les coordonnées du point H? Avec AT l'aire du triangle ABC (voir formules de Héron) Même formules avec permutations pour les autres hauteurs. Exemple: Calcul
La loi des cosinus:
Dans le triangle rectangle ACHC, le cosinus vaut:
En remplaçant. La valeur de x est déduite immédiatement.
Pour y, il faut calculer AHA via l'aire du triangle.
Triangles semblables: ABHA et AHHC
Calculs qui conduisent à la formule indiquée.

Voir Droite d'Euler

SUITE

Hauteurs du triangle: propriétés et démonstrations

Cette page

http://villemin.gerard.free.fr/Referenc/Vocabula/GlosH/Hauteur.htm